Но кроме всего этого, Гальтон хотел доказать, что источником выдающихся талантов является только наследственность, а не "домашнее воспитание, не школа или университет и не профессиональная карьера". И кажется, действительно дело в наследственности, по крайней мере если речь идет о параметрах, избранных Гальтоном. Он, например, обнаружил, что каждый девятый из близких родственников 286 судей был отцом, сыном или братом другого судьи, в то время как доля судей в общей численности населения несравненно меньше 1/9. Более того, он выяснил, что многие родственники судей являются адмиралами, генералами, писателями, поэтами и врачами. (Гальтон явно исключал служителей церкви из числа одаренных людей.) Он был вынужден с разочарованием отметить, что в его выборке в неразделимой связке оказываются одаренные люди и "конгенитальные идиоты".
Однако Гальтон установил, что высокие способности сохраняются в семье ненадолго, или, как говорят физики, имеют короткий период полураспада. Он обнаружил, что только 36% сыновей именитых людей сами достигали высокого положения, а внукам это удавалось только в 9% случаев. Он пытается объяснить, почему именитые фамилии имеют тенденцию к вымиранию, ссылаясь на общеизвестный обычай жениться на наследницах. Чем они виноваты? Потому что наследницы должны происходить из неплодовитых семей, утверждает Гальтон; если бы они имели большое число братьев и сестер, фамильное состояние делилось бы на всех и они не имели бы статуса "наследниц". Это было неожиданное утверждение в устах человека, который жил в комфорте после того, как поделил наследство своего отца с шестью братьями и сестрами.
***
Прочитав "Наследственную одаренность", Чарлз Дарвин сказал Гальтону: "Не думаю, что мне приходилось читать что-нибудь более интересное и оригинальное... примечательная книга". Дарвин советовал продолжить анализ статистических данных о наследственности, но Гальтона не нужно было подстегивать. Дело по разработке новой науки евгеники шло полным ходом, и он был полон страстного желания выявить и сохранить то, что он называл лучшим в человечестве. Гальтон хотел, чтобы лучшие люди имели больше потомства, а бездарности проявляли сдержанность.
Но на его пути упорно стоял закон об отклонениях от среднего. Нужно было как-то объяснить различия внутри нормального распределения. Гальтон понимал, что прежде всего для этого нужно выяснить, почему данные распределяются по колоколообразной кривой. Поиски ответа на этот вопрос привели его к потрясающему открытию, влияющему ныне на принятие большинства решений, больших и малых.
О первом шаге Гальтон сообщил в статье, которая была опубликована в 1875 году; в ней он высказал предположение, что универсальность симметричного распределения относительно среднего значения может быть результатом влияний факторов, которые сами распределены нормальным образом, выстраиваясь от наиболее редких условий к наиболее частым и затем опять к наиболее редким противоположным условиям. Гальтон предположил, что даже в рамках каждого отдельного фактора влияние распределяется от самого слабого к сильному и затем опять к противоположному слабому. Суть его аргументации сводилась к тому, что "посредственные" влияния встречаются гораздо чаще, чем экстремальные, неважно, плохие или хорошие.
Гальтон продемонстрировал модель своей идеи в Королевском обществе в 1874 году с помощью приспособления, которое он назвал quincunx. Это нечто вроде игры в пинбол: наклонная доска с узкой горловиной вверху, как у песочных часов, с торчащими пониже горловины двенадцатью штырьками. На противоположном широком конце лотка ряд небольших ячеек. Стоит сыпануть дроби, и она, натыкаясь на штырьки, падает вниз, заполняя расположенные внизу ячейки в полном соответствии с распределением Гаусса - большая часть дробинок собирается в средних ячейках, остальные в убывающих количествах заполняют крайние.
В 1877 году во время выступления с большим докладом на тему "Основные законы наследственности" ("Typical Laws of Heredity") Гальтон предложил новую модель своего приспособления. (Мы не знаем, построил ли он ее на самом деле.) В этой модели на пути дробинок после горловины устанавливались такие же ячейки, как на дне первой модели, но с отверстием на дне, до поры закрытым. Когда отверстие на дне какой-либо из этих верхних ячеек открывалось, дробинки скатывались в нижние ячейки, где и располагались, как вы уже, наверное, догадались, по закону нормального распределения.
Потрясающее открытие! Свойства любой группы, сколь угодно малой и хоть как-то отличающейся от других групп, имеют тенденцию распределяться в соответствии с колоколообразной кривой, так что большая часть группы попадает близко к центру, или, как принято говорить, к среднему. Когда все группы сливаются в одну, как это было в первом варианте модели, дробинки также располагаются в соответствии с нормальным распределением. Таким образом, нормальное распределение большой группы выявляет среднее от средних значений для малых подгрупп.
Вторая механическая модель была упрощенным воплощением идеи, к которой Гальтон пришел по ходу эксперимента, предложенного Дарвином в 1875 году. В этом эксперименте не использовались кости, звезды и даже люди. Использовался сладкий стручковый горох. Сладкий горох хорошо хранится, плодовит и имеет слабую тенденцию к перекрестному опылению. В каждом стручке горошины почти одинакового размера. Взвесив и пересчитав тысячи сладких горошин, Гальтон разослал десять партий по семь упаковок разного веса, в каждой девяти друзьям, включая Дарвина, жившим в разных концах Британии, с подробными инструкциями, касающимися посадки и выращивания гороха в разных условиях.
Проанализировав результаты, Гальтон сообщил, что потомство от каждой из семи партий по весу в точности повторило распределение, которое предсказало бы его приспособление. Веса горошин, выращенных из каждой из семи упаковок внутри каждой партии, образовывали нормальное распределение, и веса горошин, выращенных из каждой партии, также образовали нормальное распределение. Этот убедительный результат не был, как сказал Гальтон, следствием "разных комбинаций незначительных влияний" [курсив Гальтона. - П.Б.]. Скорее, "процессы наследования... находятся под действием не малых, а очень важных влияний". Подобно тому как немногие индивидуумы в группе людей оказываются одаренными, среди их отпрысков также немногие отличаются заметными талантами; поскольку большинство людей имеют средние способности, их потомки также обречены на средний уровень. Посредственность всегда многочисленнее талантов. Последовательность малых-больших-малых размеров горошин, образующая нормальное распределение, убедила Гальтона, что доминирующим фактором, определяющим свойства потомства, являются качества родителей.
Как свидетельствует приведенная ниже таблица распределения горошин первого и второго поколений по диаметру, эксперимент выявил кое-что еще.

Заметьте, что разброс диаметров среди родительских семян больше, чем у потомства. Средний диаметр родительских горошин был 0,18 дюйма с разбросом от 0,15 до 0,21 дюйма, или по 0,03 дюйма справа и слева от среднего значения. Средний диаметр выращенных горошин оказался равным 0,163 дюйма с разбросом от 0,154 до 0,173 дюйма, или по 0,01 дюйма справа и слева от среднего значения. Потомство распределено в более узком интервале, чем родительское поколение.
На основе этого эксперимента Гальтон предложил общий принцип, получивший название регрессии, или схождения к среднему. "Схождение, - писал Гальтон, - это тенденция идеально среднего второго поколения отойти от родительского типа, возвращаясь к тому, что можно грубовато, но, по-видимому, верно назвать усредненным наследственным типом". Если бы этот процесс схождения не срабатывал, то есть если бы (в нашем случае) большие горошины продуцировали бы еще бóльшие, а малые - еще меньшие, то в мире не осталось бы никого, кроме карликов и гигантов. Природа из поколения в поколение становилась бы все более причудливой, стремясь к абсолютной нестабильности или выходя за такие пределы, о которых не хочется и думать.
Гальтон подытожил результаты этих исследований в одном из своих наиболее красноречивых и выразительных высказываний:
"Ребенок наследует частично от своих родителей, частично от их предков... Чем дальше мы возвращаемся назад по его генеалогическому древу, тем большее число предков и вариаций выявляется в его наследственности, пока они не перестанут отличаться от столь же многочисленной случайной выборки, произвольно взятой из расы... Этот закон наносит сильный удар по представлениям о простом наследовании какого-либо таланта. <...> Закон симметричен: он касается наследования как пороков, так и добродетелей. Охлаждая экстравагантные надежды одаренных родителей на то, что их дети унаследуют все их таланты, он не менее убедительно рассеивает их опасения относительно возможного наследования их слабостей и болезней"
Элегантность формулировки не могла сделать этот вывод приятным для Гальтона, но он стимулировал его усилия по разработке евгеники. Само собой напрашивалось решение усилить влияние "усредненного наследственного типа" за счет ограничения воспроизводства потомства на нижнем конце шкалы; нужно было просто отсечь левую ветвь нормального распределения.
Гальтон нашел еще одно подтверждение схождения к среднему в эксперименте, о котором он рассказал в 1885 году по случаю его избрания президентом Британской ассоциации развития науки. Для этого эксперимента он собрал огромное количество данных о людях, которые он получил в ответ на публичное предложение снабдить его информацией за определенную плату. Он проанализировал данные о 928 взрослых детях, рожденных от 205 родительских пар.
На этот раз Гальтон занялся сравнением роста родителей и детей. Так же как и в эксперименте со сладким горошком, он и в этом обследовании поставил своей целью проверить, как это частное свойство передается по наследству. Чтобы скорректировать для целей анализа различие в росте между мужчинами и женщинами, он умножал рост женщины на 1,08, складывал показатели роста обоих родителей и делил на два. Он назвал эту величину "средним ростом родителей". Ему нужно было также быть уверенным в отсутствии тенденции к женитьбе высоких мужчин на высоких женщинах, а маленьких на маленьких; его вычисления были "достаточно скрупулезны", чтобы исключить наличие такой тенденции
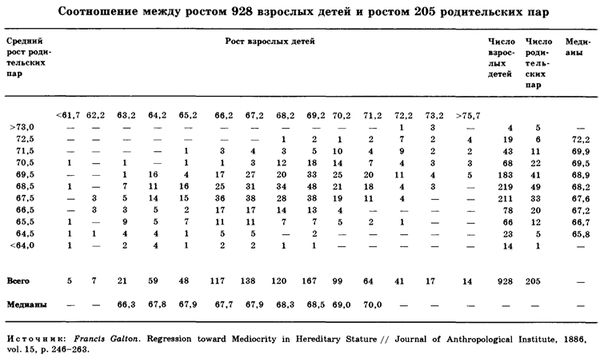
Как видно из таблицы, результат получился великолепный. Структура чисел по диагонали от левого нижнего угла до правого верхнего показывает, что у высоких родителей вырастают высокие дети и наоборот - наследственность имеет значение. Группы больших чисел в центральной части таблицы позволяют сделать вывод, что распределение детей по росту является нормальным и что рост детей, родители которых относятся к одной группе роста, также описывается нормальным распределением. И наконец, сравним самую правую и самую левую колонки. ("Медиана" означает, что в половине группы люди были выше, а в половине - ниже этого числа.) Дети всех родителей, средний рост которых был выше 68,5 дюйма, в среднем оказались ниже своих родителей; дети всех родителей, средний рост которых был ниже 68,5 дюйма, в среднем оказались выше своих родителей. Совсем как в эксперименте со сладким горошком.
Упорядоченность нормального распределения и наличие сходимости позволили Гальтону вычислить другие показатели - например, долю высоких родителей, дети которых выше своих сверстников, но ниже родителей. Когда профессиональные математики подтвердили его результаты, Гальтон написал:
"Я еще никогда не испытывал такого глубокого уважения к величественной и непререкаемой власти математического анализа"
Подход Гальтона в конце концов привел к разработке понятия корреляции, которая измеряет, насколько тесно связаны между собой изменения двух величин, будь то размеры родителей и детей, количество осадков и урожай, инфляция и процентные ставки или цены на акции General Motors и Biogen.
***
Карл Пирсон, главный биограф Гальтона и сам выдающийся математик, заметил, что Гальтон совершил "революцию в наших научных представлениях, [которая] изменила философский подход к науке и даже к самой жизни". Это не преувеличение: идея схождения к среднему сработала как динамит. Гальтон превратил статическое понятие вероятности, базирующееся на случайности и законе больших чисел, в динамическую концепцию, описывающую процесс, в котором преемникам крайних предопределено присоединиться к толпе в центре. Изменение и движение от внешних границ к центру постоянно, неизбежно и предсказуемо. Учитывая динамические свойства этого процесса, нельзя и помыслить, что его результатом будет что-либо, кроме нормального распределения. Тенденция всегда направлена к среднему, к восстановлению "нормальности", к среднему, или среднестатистическому, человеку Кветеле.
Принцип схождения к среднему объясняет почти все разнообразие поведения в условиях риска и прогнозирования. Этот принцип сквозит в поговорках типа: "Не всё коту масленица", "С высоты больнее падать", "Карта не лошадь, к утру да придет". Именно эту предопределенность событий имел в виду Иосиф, когда предсказал фараону, что за семью тучными годами последуют семь тощих лет. Об этом же думал Д. П. Морган, когда говаривал, что "рынок переменчив". Это кредо так называемых контрапунктных инвесторов, которые всегда работают в противофазе: когда они говорят, что цена акций завышена или занижена, то имеют в виду, что страх или жадность побудили толпу поддерживать цену на акции, не соответствующую их внутренней ценности, к которой цена непременно вернется со временем. Именно на это уповает проигрывающий игрок - карта не лошадь, к утру да придет. Именно это имеет в виду мой врач, когда говорит, что "потерпи" и всё пройдет. И именно с этой точки зрения воспринимал события Герберт Гувер, когда в 1931 году, ободряя сограждан, говорил, что процветание уже за углом, - к несчастью для него и других, он был не прав, середина находилась не там, где он предполагал.
Фрэнсис Гальтон был гордый человек, правда он ни разу не пережил падения. Его достижения получили широкое признание, и он прожил долгую, насыщенную жизнь. Став вдовцом, он сохранил любовь к путешествиям и продолжал писать, наслаждаясь обществом родственницы, которая была намного моложе его. Он никогда не позволял своему увлечению числами и фактами заслонить прелести жизни, и его чрезвычайно радовало ее разнообразие:
"Трудно понять, почему статистики обычно ограничиваются исследованием Среднего и не наслаждаются более широким взглядом на мир. Их души кажутся такими же закрытыми для прелести разнообразия, как у жителя какого-нибудь английского графства, чьи воспоминания о Швейцарии сводятся к тому, что, если бы ее горы сбросить в озера, швейцарцам удалось бы одним движением избавиться сразу от двух напастей"
Глава 10
Стручки и риски
Понятие схождения к среднему значению породило многие системы принятия решений с их философскими обоснованиями. И понятно почему: превращение большего в бесконечно большое или малого в бесконечно малое маловероятно. До небес деревья не растут. Уступая, как водится, искушению экстраполировать тенденции прошлого в будущее, нужно помнить о горошинах Гальтона.