Моргенштерн родился в Германии в 1902 году, но вырос и получил образование в Вене. К 1931 году он был уже достаточно признан как экономист, чтобы стать преемником Фридриха фон Хайека (fon Hayek) на посту директора престижного Венского института исследований делового цикла. Хотя он был христианином с примесью антисемитизма, в 1938 году, после вторжения Германии в Австрию, он уехал в Соединенные Штаты и скоро нашел место на экономическом факультете в Принстоне.
Моргенштерн не верил в возможность использования экономической науки для предсказания деловой активности. Он доказывал, что потребители, бизнесмены и политики учитывают прогнозы и в соответствии с ними меняют свои решения и действия. Эти изменения заставляют прогнозистов изменять прогнозы, побуждая публику к новым реакциям. Моргенштерн сравнивал эту постоянную обратную связь с игрой Шерлока Холмса и профессора Мориарти, старающихся перехитрить друг друга. Отсюда следовал вывод, что в экономике статистические методы пригодны только в описательных целях, "но твердолобые, кажется, не отдают себе в этом отчета".
Моргенштерна раздражала идея о возможности идеального прогноза, господствовавшая в экономической теории XIX века. Никто, утверждал Моргенштерн, не может знать, что собираются делать все остальные в любой данный момент: "Неограниченный прогноз и экономическое равновесие взаимно несовместимы". Фрэнк Найт высоко оценил этот вывод и предложил перевести статью Моргенштерна с немецкого на английский.
Кажется, Моргенштерн был лишен шарма. Нобелевский лауреат Пол Самуэльсон (Samuelson), автор самого популярного в течение нескольких десятилетий учебника по экономике, так писал о нем: "Наполеоновский комплекс... постоянно ссылается на авторитет каких-то физиков или других ученых". Другой современник утверждал, что принстонские экономисты "просто терпеть не могли Оскара". Да и сам Моргенштерн жаловался на недостаток внимания к своему любимому детищу. После посещения Гарварда в 1945 году он заметил, что "никто из них" не проявил никакого интереса к теории игр. В 1947 году его огорчил экономист Репке, назвавший теорию игр "досужей венской болтовней", а в 1950 году при посещении группы выдающихся экономистов в Роттердаме он обнаружил, что они "знать ничего не хотели о [теории игр], потому что она их раздражает".
Моргенштерн в свою очередь презирал лишенную строгости трактовку Кейнсом проблемы определенности и отзывался о его "Общей теории" как о "просто чудовищной работе", но, даже будучи энтузиастом использования математических методов в экономическом анализе, постоянно жаловался на свои проблемы с новыми материалами, которые подсовывал ему фон Нейман. К фон Нейману Моргенштерн относился с благоговением. "Он загадочный человек, - написал он как-то. - Столкнувшись с чем-то научным, он весь загорается, проясняется, оживает, потом гаснет, погружается в спячку, ведет поверхностные сумбурные разговоры... В нем есть что-то непостижимое".
***
Перспектива увязать холодный математический расчет теории игр с коллизиями экономики показалась заманчивой и математику, интересующемуся экономикой, и экономисту, увлеченному математикой. Дополнительным стимулом к их сотрудничеству послужило разделяемое обоими ощущение того, что, говоря словами Моргенштерна, использование математики в экономике пребывало тогда "в плачевном состоянии".
Действовали здесь и высшие мотивы: стремление сделать математику столь же мощным инструментом анализа общества, каким она проявила себя в естественных науках. Но если в наши дни такое стремление приветствовалось бы большинством представителей общественных наук, в конце 1940-х годов оно, вероятнее всего, и было главной причиной отторжения самой идеи применения теории игр. В то время академическим курятником правил Кейнс, а он считал невозможным математическое описание человеческого поведения.
"Теория игр и экономическое поведение" не теряла времени на апологию применения математических методов в ходе принятия экономических решений. Фон Нейман и Моргенштерн отвергли как "совершенно ошибочный" аргумент, будто человеческие и психологические аспекты экономики препятствуют использованию математического анализа. Указывая на то, что математику начали использовать в физике только в XVI веке, а в химии и биологии - в XVIII, они утверждали, что перспективы математизации этих наук "в эти ранние периоды вряд ли могли быть лучшими, чем в экономике - mutatis mutandis - сегодня".
Фон Нейман и Моргенштерн отвергали возражения, основанные на том, что их строгие математические операции и упор на кван-тификацию являются нереалистическими упрощениями, потому что "рядовой человек... осуществляет экономическую активность в сфере господства неопределенности". Ведь в конце концов свет и тепло люди тоже воспринимают нечетко:
"Чтобы превратить физику в науку, эти явления (тепло и свет) нужно было измерить. А в результате люди начали использовать - прямо или косвенно - результаты таких измерений даже в повседневной жизни. То же самое может случиться в будущем и в экономике. Когда с помощью теории, использующей [измерения], удастся достичь более полного понимания человеческого поведения, человеческая жизнь может существенно измениться. А это означает, что изучение этих проблем не обязательно представляет собой упадок науки"
***
В "Теории игр и экономическом поведении" анализ начинается с простого примера: человек выбирает между двумя альтернативами, как при выборе между орлом и решкой в игре в "чет и нечет". Но на этот раз фон Нейман и Моргенштерн проникают значительно глубже в природу принятия решений, заставляя человека делать выбор не между двумя простыми возможностями, а между двумя комбинациями событий.
Они рассматривают пример с человеком, который предпочитает кофе чаю, а чай молоку. Ему задают вопрос: "Что ты предпочтешь - чашку кофе или стакан, в котором с шансами 50 на 50 будет чай или молоко?" Естественно, он выберет чашку кофе.
А если сменить его предпочтения и задать тот же вопрос? Пусть на этот раз он предпочитает молоко и чаю, и кофе, но все-таки лучше кофе, чем чай. Теперь выбор между гарантированным кофе и возможностью с равной вероятностью получить чай или молоко становится менее очевидным, чем в первом случае, потому что неопределенный исход сулит ему выполнение главного желания (молоко) или же то, что ему нужно меньше всего (чай). Изменяя вероятности нахождения в стакане чая или молока и спрашивая, в какой момент для человека гарантия получения кофе и игра на получение молока с риском получить вместо него нежеланный чай станут одинаково предпочтительны, мы можем получить количественную оценку - фиксированное число - для измерения степени предпочтительности молока, кофе и чая.
Пример становится более наглядным, если перейти к технике измерения выгоды - степени удовлетворенности - от обладания одним долларом по сравнению с выгодой от получения второго доллара, то есть обладания двумя долларами. Теперь для человека лучшим исходом должно быть обладание двумя долларами, которое мы поставим на место получения молока в предыдущем примере; отсутствие денег займет теперь место чая, как наименее благоприятного исхода, и один доллар займет место среднего по предпочтительности варианта - получения кофе.
Сделаем опыт более реалистичным и будем измерять полезность, т.е. степень удовлетворения. Пусть наш человек выбирает между гарантированным одним долларом и возможностью получить либо еще один, либо остаться без ничего.
С вероятностью 50% человек получает два доллара и с вероятностью 50 - ноль, то есть математическое ожидание в игре равно одному доллару. Если человек скажет, что ему безразлично, играть ли, чтобы с равными шансами получить два доллара или ничего, или получить без игры один доллар, можно считать, что он нейтрален к риску при столь малых ставках. В соответствии с формулой, предложенной фон Нейманом и Моргенштерном, вероятность самой желанной возможности - в этом случае получить два доллара - определяет, насколько человек предпочитает один доллар вместо нуля по сравнению с тем, насколько он предпочитает два доллара вместо нуля. Здесь 50% означают, что его предпочтение получить один доллар вместо нуля составляет половину от его предпочтения получить два доллара вместо нуля. В такой ситуации полезность двух долларов вдвое больше полезности одного доллара.
Ответы других людей или при других обстоятельствах могут сильно отличаться. Посмотрим, что произойдет, если мы увеличим ставки и изменим вероятности в игре. Предположим теперь, что этот человек безразличен к альтернативе гарантированно получить 100 долларов или игре с 67% вероятности получить 200 долларов и с 33% вероятности не получить ничего. Математическое ожидание в этой игре составляет 133 доллара; иными словами, предпочтительность гарантированного исхода - получения 100 долларов - теперь больше, чем когда речь шла только о паре долларов. 67% вероятности получения 200 долларов означают, что его предпочтение получить 100 долларов вместо нуля составляет две трети от предпочтения получить 200 долларов вместо нуля: полезность от первых 100 долларов выше, чем полезность от последующих 100 долларов. Полезность большей суммы уменьшается, когда сумма денег, подвергающаяся риску, увеличивается с однозначного числа до трехзначного.
Если все это кажется вам знакомым, то так оно и есть. Рассуждение здесь то же самое, что и при вычислении "эквивалента определенности", который мы получали из фундаментального принципа Бернулли, утверждавшего, что полезность от увеличения богатства обратно пропорциональна количеству уже имеющегося богатства (см. гл. 6, с. 123-124). В этом суть избежания риска - насколько мы готовы принимать решения, способные побудить других принять решения, результаты которых будут неблагоприятны для нас. Эта линия анализа ведет от фон Неймана и Моргенштерна прямо к классическим рациональным методам, потому что разумные люди всегда ясно понимали свои предпочтения, неуклонно следовали им и представляли их себе именно так.
***
Алан Блиндер (Blinder), многолетний сотрудник Принстонского экономического факультета, соавтор популярного учебника по экономике и вице-председатель Совета управляющих Федеральной резервной системы с 1994-го по 1996 год, предложил интересный пример из теории игр. Пример появился в статье, опубликованной в 1982 году. Он посвящен вопросу о том, возможна ли или даже желательна ли координация между денежной политикой, которая включает в себя контроль величины краткосрочного процента и денежного предложения, и фискальной политикой, определяющей сбалансированность расходов федерального правительства и налоговых поступлений.
Участниками игры являются руководители Федеральной резервной системы (ФРС) и политики, определяющие соотношение между расходами и налоговыми доходами федерального бюджета. Основной задачей руководства ФРС является контроль за инфляцией, в силу чего они предпочитают политику охлаждения экономики политике ее разогрева. Срок службы членов Совета управляющих ФРС - 14 лет, а президент Федерального резервного банка сохраняет свою должность вплоть до ухода на пенсию, - это в значительной степени защищает их от политического давления. С другой стороны, политики регулярно переизбираются, так что им выгоднее сражаться за подогрев, а не за охлаждение экономики.
В ходе игры противники стараются принудить друг друга к принятию неприятных решений. Руководители ФРС хотели бы, чтобы сумма налоговых поступлений была больше суммы федеральных расходов, что предупреждает возникновение бюджетного дефицита. Профицит бюджета является средством сдерживания инфляции и, следовательно, защищает руководителей ФРС от упреков в плохой работе. Политики, которые беспокоятся о переизбрании, предпочли бы, чтобы ФРС удерживала процентные ставки на низком уровне, денежное предложение - на высоком. Такая политика стимулирует деловую активность и занятость населения и может избавить конгресс и президента от бюджетного дефицита. Каждая сторона не хочет делать то, чего хочет другая.
Блиндер построил матрицу, показывающую предпочтения каждой стороны в ответ на три возможных решения противоположной стороны: охлаждать экономику, ничего не предпринимать, разогревать экономику.
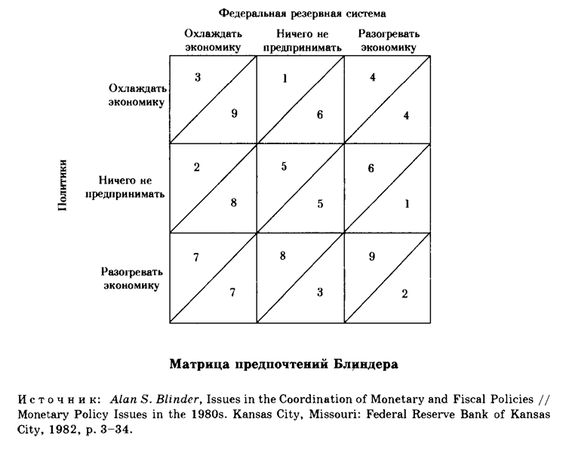
В каждом квадрате числа над диагональю представляют порядок предпочтений для руководства ФРС, числа под диагональю - для политиков.
Наиболее предпочтительные для руководства ФРС варианты (1, 2 и 3) наблюдаются в верхнем левом углу матрицы, где по крайней мере одна сторона проявляет склонность к антиинфляционной политике (охлаждение), а другая или поддерживает этот курс, или не раскачивает лодку. Руководители ФРС явно предпочитают, чтобы политики играли им на руку. Три варианта, наиболее предпочтительных для политиков, представлены в правом нижнем углу, где по крайней мере одна сторона выступает за ослабление денежной и кредитной политики, а другая или поддерживает эту идею, или не раскачивает лодку. Политики явно предпочитают, чтобы федеральные чиновники загружали деньги в экономику, а политики могли бы не сопротивляться этому, т. е. ничего не делать. Наименее желательные варианты для политиков представлены в левом столбце, а для руководства ФРС - в нижней строке. Вряд ли в этой ситуации вероятно достижение удовлетворяющего обе стороны соглашения.
Чем закончится игра? Если предположить, что отношения между чиновниками Федеральной резервной системы и политиками таковы, что сотрудничество и координация их действий невозможны, игра закончится в левом нижнем углу, где денежно-кредитная политика антиинфляционна, а бюджетно-налоговая политика ведет к дефициту бюджета. Именно так обстояло дело в первые годы президентства Рейгана, когда Блиндер писал эту статью.
Почему такой исход, а не другой? Во-первых, обе стороны здесь проявили свой характер - жесткая денежная политика ФРС и щедрые политики. Мы полагаем, что чиновники ФРС не могут убедить политиков в пользе бюджетного профицита, а политики в свою очередь не могут убедить руководство ФРС снизить процентные ставки; ни одна сторона не имеет ни малейшего желания ни уступить, ни занять нейтральную позицию.
Посмотрите, что происходит сверху и справа от этих двух семерок. Обратите внимание, что под диагоналями (предпочтения политиков) выше по левой вертикали нет ни одного числа, меньшего семи, и что выше диагоналей (предпочтения ФРС) справа по нижней горизонтали тоже нет ни одного такого числа. Коль скоро руководство ФРС склонно к охлаждению, а политики - к разогреву экономики, обе стороны вынужденно заключают лучшую из худших сделок.
Это не случай в правом верхнем углу, где жесткая бюджетная политика обеспечивает бюджетный профицит. Проследив налево по горизонтали и над диагоналями, мы заметим, что порядок предпочтительности обоих результатов для руководства ФРС выше четырех: они скорее ничего не предпримут или ужесточат денежную политику, чем пойдут на политику разогрева экономики, которая может привести к инфляции. У политиков другая перспектива. Глядя вниз по вертикали ниже диагоналей, мы заметим, что ранг этих решений выше четырех: политики скорее соглашаются бездействовать или пойти на дефицит бюджета, чем согласиться с политикой, которая может для них обернуться потерей голосов избирателей на следующих выборах из-за всплеска безработицы.
Этот исход известен как равновесие Нэша, по имени Джона Нэша (Nash), другого принстонца и одного из лауреатов Нобелевской премии за 1994 год за вклад в теорию игр. Равновесие Нэша обещает хоть и стабильный, но не оптимальный исход. Очевидно, обе стороны предпочтут почти что угодно, только не это. Однако они не смогут добиться лучшего соглашения, пока не пойдут на взаимные уступки и не выработают совместно общую политику, которую каждая сторона поддержала бы или осталась по отношению к ней нейтральной, - роль, которая удержала бы их от конфронтации. Этот пример принципиально отличается от ситуации, сложившейся в 1994 году, когда ФРС пошла на сокращение денежной массы, а политики вопреки обыкновению были готовы этому не препятствовать.
Игра Блиндера дает ясное представление о поведении по отношению друг к другу соперничающих сил в Вашингтоне. Она может быть использована и для описания множества других ситуаций. Сбросить бомбу, ничего не делать или искать мира. Снизить цены, ничего не делать или поднять цены. Торговаться с учетом своих карт и вероятности, пасовать или блефовать в покере.