Как строить деревья целей
Методика построения дерева целей состоит в том, что, определив главную цель, выстраивают иерархию целей более низкого ранга. Именно их реализация приводит к достижению главной цели. В чём-то эта работа аналогична процессу построения причинно-следственных цепочек. Последовательно задаются вопросы "Как получить?" или "Что для этого нужно?", обращённые к исходно поставленной цели.
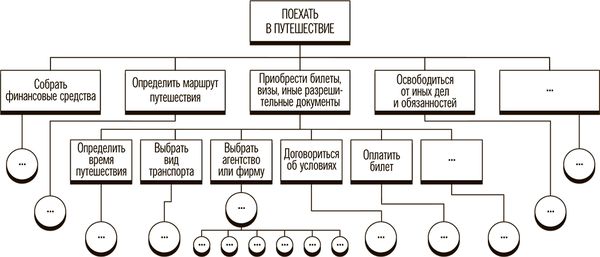
Допустим, наша главная цель - поехать в путешествие. Её достижение будет зависеть от того, сможем ли мы добиться выполнения ряда подчинённых целей второго уровня:
• Определить маршрут путешествия.
• Собрать финансовые средства.
• Приобрести билеты, визы, иные разрешительные документы.
• Освободиться от иных дел и обязанностей.
• …
Построение этой иерархии может быть продолжено. Например, выберем цель - приобрести билеты. Для её достижения нам надо будет достичь целей ещё более низкого, уже третьего (считая от главной цели) уровня:
• Определить время путешествия.
• Выбрать вид транспорта.
• Выбрать агентство или фирму.
• Договориться об условиях.
• Оплатить билет.
• …
Дерево целей (рис. 8) можно строить и далее, продолжая движение от общего к частному. Приведенный выше пример показывает: действия, позволяющие достичь цели более высокого уровня, выступают в качестве целей для действий более низкого уровня.
В итоге на самом нижнем уровне получаем перечень целей, для достижения которых могут быть выбраны конкретные технические (или иные) средства. При решении организационных задач построение такой иерархии позволяет оценить риски проекта. При решении изобретательских задач деревья целей строятся в первую очередь для того, чтобы понять, какие подцели не могут быть реализованы с помощью доступных средств. После построения дерева получается комплекс задач, которые предстоит решить.
Использование деревьев целей при анализе ИС
Такой подход к формированию задач возник в 60-х годах XX века, когда в США были построены всеобъемлющие деревья целей для проектирования сложной военной техники. Всемирную известность этот инструмент получил после успешного планирования исследований космического пространства. Начавшись с определения главной цели, пройдя через выявление нескольких фундаментальных подцелей, задающих необходимость изучения Луны, планет, ближнего и дальнего космоса, это дерево детализировалось, превратившись постепенно в перечень из нескольких тысяч узкотехнических целей, по сути - заданий на разработку конкретных технических устройств и материалов, обладающих заданными характеристиками.
Такая фундаментальная предварительная работа позволяет уже на начальном этапе видеть весь перечень технических задач, а значит, эффективно планировать необходимые ресурсы для их решения. Этот инструмент эффективен также при работе по выбору изобретательской задачи. Он позволяет увидеть полный спектр целей, в первом приближении оценить трудозатраты, необходимые для достижения главной цели.
Дерево целей - аналитический инструмент выявления полного перечня целей, которых необходимо достичь для получения исходно заданной цели.
Зафиксируем ещё раз: с помощью дерева целей определяются полный набор средств, необходимых для достижения главной цели, и связи между этими средствами.
Упражнение 7
1. Постройте дерево целей для главной цели: издать сборник стихов молодых поэтов вашего региона.
2. Придумайте какую-либо главную цель и постройте для неё дерево целей.
7. Идеальность
Идеальная тс
В каком направлении надо двигаться в поисках решения? Где найти ориентиры, позволяющие сделать это движение успешным? Какое решение считать лучшим?
Рассмотрим реальные ситуации.
В XVII веке на реке Урал построили множество плотин с водяными колёсами, приводившими в движение фабричные станки. В XIX веке фабрики оснастили паровыми машинами, а по реке решили пустить пароход. Но как убрать сваи, вбитые в дно? Это стволы лиственницы - сибирского дерева, которое в воде не гниёт, а становится ещё более прочным. И таких стволов, крепко затянутых илом, из дна реки торчит множество. Предлагали различные проекты: спустить в колоколе на дно людей с пилами, или собирать большой плот вокруг каждой сваи и тянуть её вверх, или помещать сваю в трубу и растворять её кислотой… Но победил проект, в котором сваи были вытянуты сами собой. Вернее, не совсем сами, их помогла выдернуть река. К каждой свае крепкими канатами привязали брёвна и оставили их плавать на поверхности воды. Зимой эти брёвна вмёрзли в лёд, а весной, во время ледохода, они двинулись с места и, увлекаемые огромной энергией реки, выдернули из дна сваи…
Ещё один пример из тех же времён.
Купили промышленники паровую машину, привезли к фабрике, осталось только по мосту через реку переехать, но оказалось, что мост для такой нагрузки слабоват - может и рухнуть. Разобрали машину, почти все детали перевезли по отдельности, но самую большую - паровой котёл - перевезти не получается. Неужели строить новый мост? Нет, мастера-выдумщики нашли другое решение - заставили чугунный котёл переплыть реку самостоятельно. Для этого заткнули в нём все отверстия, скатили котёл в воду и потянули за лодками…
А вот история уже из наших дней.
На предприятии выпускали шарики для подшипников. Пришёл заказ - изготовить металлические шарики, полые внутри. Изготовили. Снаружи шарики проверили стандартными методами - все они совершенно круглые, одинакового размера и веса. Но заказчик требует, чтобы у шариков внутренние пустоты тоже были расположены строго по центру. Как же отобрать только такие шарики? Может быть, просвечивать каждый шарик в рентгеновских лучах и изучать полученные снимки? Но это дорого и займёт много времени. Поступили проще - запустили шарики скатываться по узкой наклонной полоске. Те шарики, в которых внутренние пустоты располагались по центру, катились строго по прямой линии. А те, у которых центр тяжести был смещён, отклонялись вбок и падали в стоящий внизу контейнер для брака.
Что объединяет все эти решения? Изобретатели в максимальной степени использовали ресурсы, имеющиеся в совершенствуемой системе или вокруг неё, как бы заключили своеобразный договор с природой о применении для работы её сил. Река сама, без домкратов и пил вытянула сваи; котёл сам, без моста и парохода переправился через реку; бракованные шарики сами отделились от качественных.
Впрочем, не совсем сами. Им пришлось немного помочь. Заметьте, не делать всю работу самостоятельно, а помочь сделать так, чтобы эту работу выполнили силы природы. Пожалуй, в этом и состоит главное мастерство изобретателей - сделать так, чтобы работа выполнялась сама. Чем меньшими усилиями человека выполняется работа, тем сильнее изобретение.
Человек издавна изобретает. Добыть и приготовить пищу, передать на большое расстояние информацию, отвести воду от жилища… Для этого он создаёт технику: различные устройства, приборы, машины. Но техника сама по себе человеку не нужна - нужен эффект, который она производит, нужен результат. Чем проще будет ТС, тем лучше. Получается, что предел развития техники - это получение полезного результата вообще без ТС.
Этот внешне парадоксальный вывод и лёг в основу понятия идеальной технической системы. Понятие идеальной ТС предложил Г. С. Альтшуллер.
Под идеальной понимается такая техническая система, затраты на получение полезного эффекта в которой равны нулю. При этом затратами будем считать энергию, материалы, которые нужны для создания системы и её функционирования, занимаемое пространство… Образ идеальной системы позволяет сконцентрировать внимание разработчика только на ожидаемом полезном эффекте, лучше осознать запросы потребителя. Идеальная машина - это машина, которой нет, а функция её выполняется.
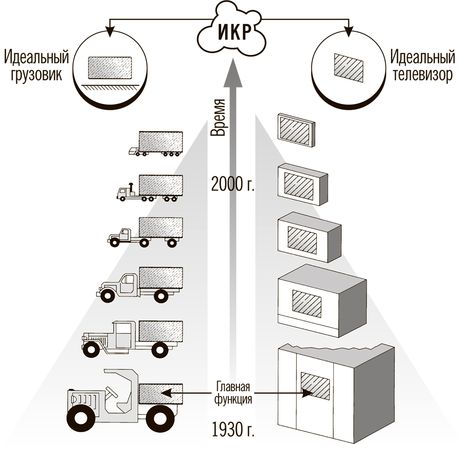
Идеальный телевизор - это получение высококачественного изображения без технического устройства.
Идеальный автомобиль - это самостоятельное перемещение грузов.
Как видим, система здесь описывается через свою функцию. Пределом развития ТС является выполнение полезной функции без всяких затрат. Именно это можно рассматривать как конечную цель её развития. Такой подход к описанию будущего очень удобен. Мы можем пока не знать, из каких материалов будет сделана будущая система, какие физические принципы в ней заложены, но мы знаем, к какому пределу она стремится. Каждая узкая область техники имеет собственные критерии оценки идеальности. Помимо широко известного коэффициента полезного действия применяются коэффициенты полезной загрузки площади или объёма, коэффициент полезного использования времени, коэффициент зольности топлива, коэффициент эффективности экономики и т. п.
Чем меньше затраты на выполнение функции, тем более идеальна система. Можно увеличить идеальность, используя ресурсы самой обрабатываемой ТС.
Хлеб традиционно выпекают в специальных печах. Стоимость таких печей и затраты энергии на их нагрев очень велики. Изобретатели предложили нагревать сразу само тесто. Оказалось, что для этого есть определённый ресурс - тесто электропроводно. Если через него пропустить электрический ток, то будет выделяться тепло. Теперь выпечка происходит очень быстро, прямо при движении форм с тестом по конвейеру. Печь не нужна, существенно снижаются и затраты энергии.
Идеальность обрабатывающей ТС можно увеличить, возложив на неё выполнение дополнительных функций. Так, в одном устройстве совмещают возможности двух. Например, сеялка вносит в почву не только семена, но и удобрения.
Идеальный конечный результат
Решая изобретательскую задачу, специалист по ТРИЗ ищет решение с высокой идеальностью, то есть такое, которое позволяет добиться необходимого результата с минимальными затратами. Для поиска таких решений Альтшуллер разработал специальный инструмент - оператор ИКР (идеальный конечный результат), который настраивает изобретателя на получение нужного эффекта за счёт использования доступных ресурсов.
ИКР может формулироваться по-разному. Но самая распространённая, классическая формулировка такова:
Идеальный конечный результат:Х-элемент сам выполняет требуемое действие (вместо какой-то специализированной ТС), продолжая выполнять функцию, ради которой он был первоначально создан.
При этом под названием "Х-элемент" может скрываться либо сама проблемная ТС, либо какая-то её подсистема.
В море недалеко от берега установлены буи. Они обозначают линию, которую нельзя пересекать судам. Буи в темноте светятся - на них установлены лампы и аккумуляторы. Время от времени аккумуляторы приходится менять и подзаряжать - для этого работает специальная служба. В ветреную погоду, когда море волнуется, замена аккумуляторов становится проблемой. Заказчик просит решить эту проблему. Какой путь её решения следует выбрать?
Идеальная система подзарядки - когда системы нет вообще, а её функция выполняется. Сформулируем ИКР: буй сам заряжает аккумулятор, продолжая выполнять функцию границы зоны, разрешённой для плавания.
Можно ли реализовать ИКР в данном конкретном случае? Для этого нужно найти ресурс - бесплатную энергию, которую можно преобразовывать в электрическую. Нетрудно догадаться, что такой ресурс есть - это энергия волн. Есть простые готовые устройства, с помощью которых качающийся на волнах буй будет сам по себе заряжаться. А система замены аккумуляторов с применением рискованного человеческого труда будет не нужна.
Дана изобретательская ситуация: необходимо повысить идеальность комнатного очистителя воздуха. Что может быть Х-элементом?
• ИКР-1: воздух сам отделяет от себя пыль.
• ИКР-2: фильтрующий элемент сам (без вентилятора и корпуса) очищает воздух.
• ИКР-3: стенка квартиры сама очищает воздух от пыли.
Упражнение 8
1. Мытьё окон - утомительная работа, которой приходится заниматься постоянно, иначе оседающая на стекле пыль очень скоро сделает окно непрозрачным. В высотных зданиях мытьё окон к тому же просто опасно. Придумайте, как повысить идеальность этой операции.
2. Длительность моментов, когда человек переживает острые ощущения, очень мала. Нужно сделать много снимков, чтобы "поймать" нужный момент и получить фотографию человека в таком состоянии. Как, не делая большого количества снимков, сфотографировать человеческое лицо в нужный момент, например при катании на экстремальных аттракционах? Сформулируйте ИКР.
3. Весной, когда разливается река, может возникнуть необходимость быстро возвести дамбу. Завозить для этого специальные строительные материалы (бетон, камень, металлические листы) долго и дорого. А подручные материалы (песок, почва), к сожалению, очень быстро размываются потоками воды. Как повысить скорость и эффективность строительства такой временной дамбы?
8. Ресурсы
Ресурсы для решения задач
Чтобы получить высокоидеальное решение, то есть обеспечить выполнение функции с минимальными затратами, необходимо найти соответствующие ресурсы в само́й проблемной системе или в её окружении.
В предыдущей главе рассматривалась задача об удалении вбитых в дно реки свай. Какие же ресурсы можно было найти, чтобы убрать сваи?
Можно было тянуть сваи с берега, используя людей или конные упряжки. Для этого требуются рабочие, лошади, длинные прочные канаты, лодки, чтобы крепить канаты на сваях, и т. д. Можно было соединить несколько плотов вокруг сваи, раскачать её с этих плотов и потом рычагом вытянуть из грунта. Плоты нужны большие и прочные, чтобы при вытягивании свай они не ушли под воду, не развалились. И нужны люди - сильные и в достаточном количестве. Предлагались и экзотические решения: спустить в колоколе на дно людей с пилами или поместить сваю в трубу и растворить её кислотой.
В действительности был использован идеальный ресурс, самый мощный источник энергии - сама река. Сила её течения превосходит силы всех рабочих, вместе взятых, к тому же этот ресурс совершенно бесплатный и практически неисчерпаемый. Реку можно использовать для удаления свай разными способами. Например, затопить вокруг сваи несколько бочек, привязав к ним мешки с камнями, а затем, прикрепив бочки верёвками к свае, обрезать "якоря". Всплывающие бочки, если они достаточно велики, выдернут сваю. В этом случае работу выполнит подъёмная сила воды. Можно использовать и кинетическую энергию течения воды - сделать "водяной парус". Для этого придётся опустить в воду полотнище, привязав его к сваям, и позволить течению реки, наполняющему этот "парус", выворотить сваи из дна. А можно, как и было сделано, закрепить к сваям брёвна и, дождавшись ледохода, наблюдать с бережка, как движущийся лёд вырвет и унесёт сваи.
Итак, решение любой проблемы, как в приведённом выше примере, во многом зависит от нахождения и грамотного использования ресурсов.
Ресурс это пространство, время, вещество, энергия, информация, которые могут быть использованы для решения задачи.
Высокоидеальные решения получаются с использованием тех ресурсов, которые уже есть в системе. Если нужного ресурса нет, его зачастую можно получить, изменяя существующие. Например, если для решения задачи нужно использовать жидкость, а в наличии есть только твёрдые вещества, жидкость можно получить расплавлением. Находить, "вычислять" и задействовать ресурсы - это одна из важных составляющих умения решателя.
Виды ресурсов
Классификацию ресурсов полезно знать, чтобы вести их поиск не случайным образом, а системно. Различают энергетические и вещественные, пространственные и временны́е, информационные ресурсы.
Энергетические ресурсы. Практически в каждой ТС существуют источники энергии и силы - как явные, так и скрытые. Даже в такой простой ТС, как свая, можно обнаружить продольную и поперечную силы упругости материала, сопротивляющиеся давлению, вес сваи, энергию горения древесины. В надсистеме "река" есть кинетическая энергия движения воды, вес воды, сила Архимеда… При взаимодействии разных систем тоже могут порождаться определённые силы: давление потока на сваю, сила трения и нагрев соприкасающихся тел.
Вещественными ресурсами могут являться все вещества, которые есть в системе или её надсистемах. В задаче об удалении свай вещественным ресурсом можно считать воду в реке, канаты, тягловых лошадей, камни и песок на берегу и дне.
Пространственные ресурсы - это пространство, которое может быть использовано для решения задачи. "Пустота", особенности формы объектов, которые можно применить для изменения исходной системы или для повышения эффективности её эксплуатации. Примером использования пространственных ресурсов может служить предложение полностью забивать сваи в дно. Ресурс здесь - пространство под дном, которое обычно не принимается в расчёт при решении.