- Стоп! Ни с места!
- Что случилось? - спросил я, испуганно попятившись и, надо сказать, весьма обескураженный таким нелюбезным приёмом.
Губернатор схватился за голову.
- Он ещё спрашивает! Разве вы не видите, что чуть не наступили на задачу?!
Я посмотрел вниз и увидал полукруг из листового золота диаметром эдак сантиметров пятьдесят. Ничего себе задачки предлагают в этой стране! Подумать только, сколько драгоценного металла ушло на эту штуковину…
- Так это и есть ваша задача? - спросил я. - А в чём она заключается?
Тут наконец губернатор впервые обратил ко мне свои ясные очи, в которых сверкало откровенное злорадство.
- О, задача хитрая! На мой взгляд, даже чересчур. Но вы ведь, кажется, похвалялись её решить?
- Да, ваше вице-губернаторство, - подтвердил я скромно, но твёрдо.
- Для вашего же блага советую вам сдержать обещание, иначе придётся вам познакомиться с обитателем вон той клетки.
Я посмотрел в указанном направлении и увидел невдалеке большую, полускрытую зеленью клетку, откуда доносились какие-то странные звуки: рёв, блеяние, шипение… Мне, признаться, сразу стало как-то неуютно. Не то чтобы я усомнился в своих математических способностях, но решать задачи приятнее, знаете ли, в более миролюбивой обстановке. Однако я и вида не подал, что взволнован, и попросил моего мучителя изложить существо задачи.
- Извольте, - сказал он. - Вот вам золотой полукруг. Надо провести в нём мелом одну, да, да - одну-единственную линию, но так, чтобы она разделила его на две части, из которых большая равна квадрату радиуса этого полукруга.
- Но это же квадратура круга! - воскликнул я, похолодев. - А квадратура круга, все знают, - задача неразрешимая.
- Тем хуже для вас, - усмехнулся правитель и хотел хлопнуть в ладоши, чтобы позвать стражу.
Но тут в саду отчётливо прозвучал спокойный голосок Единички:
- Повремените, ваша светлость! Магистр пошутил. Он отлично знает, что ваша задача не имеет ничего общего с квадратурой круга. Дайте мне линейку и циркуль, и я вам докажу, что задачу эту может решить не только Магистр Рассеянных Наук, но даже его ученица.
Вице-губернатор оторопел.
- Ты? Ты - от горшка два вершка… Советую тебе оставить эту затею. Кстати, учти, что, решая эту задачу, можно пользоваться только циркулем. Линейки не полагается.
Душа у меня снова ушла в пятки. Единичка тоже, казалось, призадумалась, но потом внимательно взглянула на полукруг и улыбнулась.
- Как же я сразу не заметила, что на полукруге имеются две отметины! - сказала она с облегчением. - Одна - посередине диаметра, другая - посередине дуги. Где циркуль, ваша светлость? Велите подать его сюда.
Принесли большой школьный циркуль. Единичка вставила в него мелок, сделала с его помощью какие-то засечки, потом описала жирную дугу и торжествующе отбросила циркуль в сторону.

- Вот и всё! Большая отделённая мною часть полукруга в точности равна квадрату его радиуса.
Признаться, у меня не было уверенности в Единичкиной правоте. К сожалению, не было её и у вице-губернатора: он строгим голосом потребовал доказательств. И что бы вы думали? Единичка представила их незамедлительно!
И тут произошло нечто необычайное. Вице-губернатор прослезился от счастья, опустился перед Единичкой на одно колено и предложил ей остаться у него в должности главного математика! Разумеется, дорогая моя спутница любезно отказалась от этой чести, отговорившись тем, что ей сперва нужно окончить десятилетку.
- В таком случае, - воскликнул губернатор, - я буду ждать сколько угодно! Даже если вам вздумается сидеть в каждом классе по два года.
- Надеюсь, этого не случится! - засмеялась счастливая Единичка.
Но восхищённый правитель Сьеррахимеры никак не хотел отказать себе в удовольствии отблагодарить её, если не по-царски, то по крайней мере по-губернаторски.
- Раз уж нельзя вам оставаться здесь, - сказал он, - так разрешите мне сделать вам достойный подарок. Примите от меня это сверкающее золотое полукружие, чтобы блеск его всю жизнь напоминал вам о вашей блестящей победе.
Единичка церемонно присела (и откуда только у неё эти придворные манеры?).
- Слов нет, ваша милость, подарок действительно блестящий. Но, право же, золото мне ни к чему. Что я стану делать с таким огромным богатством?
- Было бы богатство, а уж истратить его - дело нехитрое! - засмеялся губернатор.
Но Единичка упрямо стояла на своём.
- Вижу, отблагодарить вас не так-то просто, - сказал наконец озадаченный вельможа. - Что ж, будь по-вашему. Не стану больше навязывать вам драгоценности. На сей раз я предложу вам редкость. Да, редкость, которую я недавно приобрёл за 350 тысяч колумбов - не более и не менее!
350 тысяч колумбов! Где-то я уже слышал эти слова. В голове моей возникли какие-то смутные воспоминания. Я хотел сказать об этом, но Единичка пребольно ущипнула меня за руку и заявила своему высочайшему благодетелю, что ей не терпится взглянуть на таинственную диковину.
Стоит ли говорить, что мы испытали, когда открыли принесённую по знаку губернатора шкатулку и увидали… Ах, что мы увидали! На алой бархатной подушечке лежала она - знакомая вам уникальная марка!
Только я собрался удивить губернатора, показав ему родную сестрицу его филателистической редкости, как Единичка ущипнула меня ещё больней, чем в первый раз, и заговорила сама:
- Увы, ваша светлость, я и на этот раз должна отказаться от подарка.
- Но почему?! - взревел изнемогающий от избытка благодарности губернатор.
Единичка скромно потупилась.
- Не хочу вас обижать, но дело в том, что на всём свете существуют только две такие марки.
- Ну да, - подтвердил губернатор, - одна в Терранигугу, вторая в Сьерранибумбуме.
- Почти так, - осторожно возразила Единичка, - потому что марка, хранившаяся в Терранигугу, недавно украдена.
Не может быть! - вскричал вице-губернатор, страшно побледнев. - Я об этом ничего не знал!
- Не мудрено, ваша светлость, - сказал я, - ведь уже восемь месяцев и двенадцать дней, как в Сьеррахимеру нет доступа никому со стороны!
- В самом деле, - пробормотал губернатор. - Неужели, воспользовавшись моим неведением, мне продали краденую марку?
- Судя по всему, ваша марка не из Терранигугу, - задумчиво сказала Единичка.
Губернатор вздохнул с облегчением:
- Слава богу! Значит, мне продали ту, что хранилась в Сьерранибумбуме.
- Скорей всего, так. Вопрос в том, с ведома ли владельца…
- Вы хотите сказать, что и эта марка краденая?! - снова ужаснулся губернатор.
Единичка уклончиво потупилась.
- Как знать…
- Сейчас мы это выясним! - Губернатор решительно хлопнул в ладоши. - Немедленно позвать сюда синьора Кактуса! Он продал - он пусть и отвечает!
Услыхав знакомое имя, я так и подскочил на месте, а Единичка разом забыла свои великосветские выкрутасы и затрубила что-то свирепое и воинственное. Точно она дикий индеец и собирается оскальпировать этого Кактуса… Однако увидеть его нам все же не довелось. Посланный за ним слуга вернулся один и доложил, что синьор Кактус срочно покинул Сьеррахимеру. Автомобиль его видели на шоссе, ведущем в Сьерранибумбум.
- Урррра!.. - заорал я и, подхватив Единичку, закружился с ней в неистовом танце.
- Не понимаю, чему вы радуетесь? - спросил сбитый с толку губернатор.
Чему я радуюсь? Ну, этого я ему не скажу… Но вы-то, конечно, понимаете, в чём дело! Теперь у меня все основания думать, что Кактус украл марку у синьора Альбертини и помчался заметать следы. Правда, есть тут и некая неувязка, потому что тот же Кактус каким-то образом связан с синьором Джерамини… Да, клубок снова запутывается. И всё же гордиева петля вокруг шеи преступника стягивается все туже…
- Скорей отделывайся от губернатора! - шепнул я Единичке. - Мы срочно едем в Сьерранибумбум!
Двадцать шестое заседание КРМ
возглавлял, против обыкновения, не Нулик, а Олег: во время похода в кино президент проявил излишний интерес к мороженому и совершенно обезголосел. Изо рта у него вырывались сплошные шипящие и хрипящие, что, впрочем, не мешало ему оставаться заядлым спорщиком.
Только Олег позвонил в колокольчик и открыл заседание словами: "Итак, вернёмся к нашим баранам!", как президент, хрипя и давясь, заявил, что не позволит оскорблять Магистра и Единичку.
- Действительно неудобно как-то, - поддержала его Таня. - Ну при чём тут бараны? Помнится, Магистр сам сказал что-то такое. Но относилось это к губернатору…
- Да не к губернатору оно относилось, - возразил Сева. - "Вернёмся к нашим баранам" говорят тогда, когда хотят вернуться к существу дела.
- Объяснение точное, - подтвердил я. - Остаётся выяснить, откуда пошло это иносказательное выражение.
- Понятия не имею, - честно признался Сева.
- Беда поправимая, - сказал я. - Есть такая весёлая французская пьеска "Адвокат Патлен". Появилась она давным-давно, в шестнадцатом веке. Действие происходит в суде. Слушается дело о баранах. Хитрый адвокат Патлен всё время старается запутать ясный вопрос и отвлечь от него внимание судьи. А замороченный судья то и дело восклицает: "Вернёмся же к нашим баранам!"

- Забавная, наверное, сценка! Интересно, кто её написал?
- То-то и дело, что автор неизвестен.
- Автор неизвестен, автора давным-давно нет, а бараны его все живут, - философствовал Нулик.
- По этому случаю вернёмся наконец к нашим баранам, - предложил я. - Первым долгом обсудим вопрос Единички: чего больше - натуральных чисел или их квадратов?
- Но Единичка уже ответила на него! - возразила Таня. - И Магистру вряд ли удастся её опровергнуть.
- Между прочим, - напомнил Олег, - этим вопросом мы уже занимались. В прошлом году, когда говорили о множествах…
- А ведь верно! - сказала Таня. - Вопрос Единички и в самом деле касается множеств…
- Притом бесконечных множеств, - уточнил Сева. - И Единичка, конечно же, права: раз каждое число натурального ряда можно возвести в квадрат, значит, квадратов существует ровно столько, сколько натуральных чисел, то есть бесконечное множество.
- Надо сказать, Единичка доказала это очень простым способом, - вмешался я. - Над каждым квадратом она надписала его порядковый номер, то есть попросту пересчитала их. Недаром множества, которые можно перенумеровать, называются счётными.
- А разве есть множества, которые пересчитать нельзя? - спросил Нулик.
- Конечно. Вот, например, множество точек на отрезке прямой. Оно несчётное, хотя количество точек на любых отрезках прямой всегда одинаково.
- Как же так? - прошептал Нулик, окончательно потеряв голос от изумления.
- Вот так. Где, по-твоему, точек больше: на средней линии треугольника или на его основании?
- Что за вопрос! - фыркнул Нулик. - Конечно, на основании! Ведь оно вдвое длиннее средней линии.
- Не угадал. Пусть средняя линия вдвое меньше основания, а точек и тут и там совершенно одинаковое множество.
Я нарисовал треугольник, начертил его среднюю линию и провёл из вершины с десяток лучей, которые пересекли и среднюю линию и основание.
- Как видишь, каждый луч, пересекающий среднюю линию, непременно пересечёт и основание треугольника. Таких лучей я могу провести сколько угодно через любую точку средней линии. А раз так, значит, любой точке средней линии непременно соответствует какая-нибудь точка основания. Стало быть, множество точек и тут и там одинаково. Вот что бывает, когда имеешь дело с бесконечными несчётными множествами. Здесь сплошь да рядом часть равна целому.
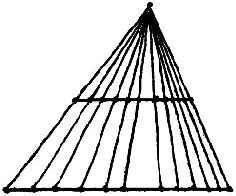
- Ну и фокус! - выдохнул Сева.
- В бесконечности такие фокусы - дело обычное.
- Да, с бесконечностью лучше не связываться, - сказал Нулик. - И вообще пора нам отправляться на индульгенцию к вице-губернатору.
- А может, всё-таки на аудиенцию? - подмигнул Сева.
- Все остришь, да зря, - остановила его Таня. - Он ни того, ни другого не знает.
- Ничего, сейчас мы его просветим. Индульгенция, дорогой президент, слово латинское. В прямом значении это милость, а вообще-то так называется у католиков церковная грамота об отпущении грехов. Вот, например, натворил ты что-нибудь и хочешь искупить свою вину. Ступай к священнику да не забудь денег прихватить - и отпущение тебе обеспечено.
- А если денег у меня нет?
- Нет, так и ходи непрощенный.
- Ну и ладно! - неожиданно рассвирепел Нулик. - Не надо мне такой индульгенции!
- Мне тоже, - серьёзно согласился Олег. - Откупаться от грехов деньгами, это не для нас с тобой! Правда, Нулик? Мы люди порядочные. Махнём-ка лучше на приём, то бишь на аудиенцию к губернатору, и займёмся задачей о золотом полукруге.
Но президента, видимо, такая перспектива не слишком устраивала. Он вдруг безмолвно замотал головой, указывая пальцем на своё горло.
- А ещё порядочный человек! - потешалась Таня. - Спорить у него голоса хватает, а как надо задачу решать - так нет его!
Она взяла циркуль, линейку, вычертила на бумаге полукруг и сделала на нём две отметки: одну посередине диаметра, другую посередине полуокружности.
- Явное нарушение! - не выдержал президент. - Во-первых, решать задачу с помощью линейки по условию нельзя, а во-вторых, полукруг должен быть золотой.
- Во-первых, - весело передразнила Таня, - обойдёшься и нарисованным полукругом. Во-вторых, к решению я ещё только приступаю. Значит, так. Требуется отделить от полукруга часть, равновеликую квадрату, сторона которого равна радиусу полукруга.
- А это и есть квадратура круга! - запрыгал на одной ножке Нулик.
- Так думает Магистр, - возразила Таня. - И он, как всегда, неправ. В задаче о квадратуре круга требуется заменить равновеликим квадратом весь круг. Мы же должны заменить квадратом всего лишь часть круга.
- Все равно, - не унимался президент, - значит, это частичная квадратура круга.
- Скорее, наоборот, - поправил я, - не частичная квадратура, а квадратура части круга. И если полный круг заменить равновеликим квадратом немыслимо, то хитро выделенную часть круга в квадрат превратить можно. Это и собирается доказать нам Таня.
Таня отмерила циркулем расстояние от конца диаметра до его середины.
- Все видят, что расстояние между ножками циркуля равно радиусу полукруга? - спросила она.
- Все видят, - сказал Нулик.
Тогда Таня воткнула иглу циркуля в левый конец диаметра и, повернув циркуль против хода часовой стрелки, засекла карандашом небольшую дугу. Потом она вставила иголку в середину полуокружности и тем же радиусом засекла другую дугу, которая пересеклась с первой.
- Теперь смотрите внимательно, - сказала Таня. - Из точки пересечения этих двух дужек тем же раствором циркуля, то есть радиусом полукруга, провожу внутри нашего полукруга дугу. Эта дуга начинается из левого конца диаметра и доходит до середины полуокружности. Таким образом, полукруг разделился на две неравные части, и площадь большей из этих двух частей равна r, то есть равновелика квадрату со стороной, равной радиусу… Пожалей своё горло, Нулик! Я и так знаю, что ты хочешь сказать, и потому прямо перехожу к доказательству.
Таня соединила концы диаметра с серединой полуокружности. Получился равнобедренный треугольник.
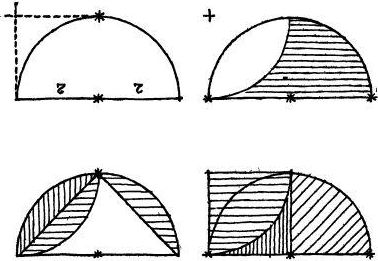
- Доказать, что боковая сторона треугольника разделила меньшую часть полукруга на два равновеликих сегмента, нетрудно. Потому пусть каждый сделает это сам. А теперь посмотрите сюда, на эти три сегмента. Все они образованы боковыми сторонами треугольника, которые одновременно и хорды полукруга. Стало быть, площади этих трех сегментов равны между собой. А раз они равны, значит, треугольник и большая часть полукруга тоже равновелики. Ведь сегмент, отнятый от треугольника слева, прибавляется к этому треугольнику справа! А так как площадь треугольника равна r (ведь основание у него 2r, высота r, а 2r·/2r=r), то значит, и площадь искомой нами части полукруга тоже равна r.
- Ловко доказано… - вздохнул Сева.
- Ловко, но длинновато, - заметил Олег. - Я бы доказал это проще.
Он тут же вычертил новый полукруг и циркулем отделил от него ту часть, что полагается. Затем на левой половине полукруга построил квадрат, приняв за сторону вертикальный радиус.
- А теперь смотрите внимательно, - продолжал Олег. - Видите, из каких частей состоят квадрат и отделённая часть полукруга?
- Видим, - прохрипел Нулик. - Они имеют по общей части и… - Тут он запнулся.
- …и по равному сектору - четверти круга, - закончил его мысль Олег.
- Вот именно. А это значит, что большая часть полукруга и квадрат равновелики, - заключил президент и добавил неожиданно чистым голосом: - Что и требовалось доказать.
- Редкий случай в медицине! - заметил Сева. - Лечение геометрией.
- А ведь в самом деле прошло! - радовался Нулик. - Ой, как легко стало! Точно с меня гордиеву петлю сняли…
- Что-то ничего о такой не слыхал, - усмехнулся Сева.
- Как это не слыхал! Почитай письмо Магистра.
- Все равно, нет гордиевой петли. Есть гордиев узел. Такое же иносказательное выражение, как "вернёмся к нашим баранам". Только баранам около четырехсот лет, а узлу более двух тысяч.
- А сам ты узнал об этом только вчера из какой-нибудь энциклопедии, - как бы невзначай проронила Таня.
- Чего и вам желаю, - отбил удар Сева, ничуть не смутившись. - И не надо мне будет тогда рассказывать, что Александр Македонский во время похода в Малую Азию попал во фригийский город Гордий, иначе - Гордион, расположенный недалеко от нынешней столицы Турции Анкары?. В городе показали Александру колесницу, у которой дышло и хомут были связаны тугим узлом, да так крепко, что развязать их не было никакой возможности. Тамошний оракул - сказали Александру - предрёк, что человек, который сумеет распутать этот узел, станет владыкой мира.
- Ну, дальше всё ясно, - сказал Нулик. - Александр, конечно, узел распутал.
- Сразу видно: не знаешь ты Александра Македонского! Он попросту вынул меч и разрубил заколдованный узел одним ударом. Отсюда "разрубить гордиев узел" значит действовать в запутанных обстоятельствах смело и решительно.