Для любой цифры, отличной от 0 и 1, среди выписанных найдется как сумма, содержащая эту цифру, так и сумма, не содержащая ее. Аналогично разбираются случаи всех остальных карточек Бабы-Яги.
Ответ. Не может.
Комментарий 1. Если бы Иван назвал вместо 7 любую другую цифру, ответы и решения остались бы прежними с точностью до конкретных выписанных сумм.
Комментарий 2. Разобранный пример показывает возможность вслух сообщить информацию так, чтобы партнер, владеющий дополняющей информацией, понял все, а случайный слушатель – ничего. Подобным образом происходят электронные платежи – банк должен узнать клиента, при этом доступ к чужому счету для жуликов должен быть максимально затруднен. Доказательствами без разглашения занимается прикладная криптография.
9.11. Участник А не может быть мирным жителем, так как в этом случае он ничего не знал бы про Д. Если бы Б был мирным жителем, то к моменту своего высказывания он знал бы только то, что А не мирный житель, и свою роль в игре. Этого недостаточно, чтобы утверждать, что Д – мафиози. Если В – мирный житель, то у него нет оснований исключать, что А и Б – мафиози, а Д – комиссар, и тогда Д знает, кто он. Поэтому и В не мирный житель. Получается, что мирные жители – Г и Д. Они оба это к моменту высказывания Г понимают, так что Г говорит правду. Участник Б лжет, поэтому он – мафиози. Кто из А и В комиссар, а кто второй мафиози, определить невозможно, оба варианта не противоречат высказываниям всех игроков.
Ответ. Б – мафиози, Г и Д – мирные жители.
Занятие 10
10.6. Если белых колпаков по-прежнему два, а черных более трех (например, 4 или 5), то все рассуждения останутся в силе. А вот если мудрецам принести три белых и три черных колпака и надеть на каждого черный колпак, третий мудрец тоже не сможет определить цвет своего колпака, но доказать это непросто. Заметим, что в таком случае после того, как все три мудреца по очереди скажут "не знаю", первый уже сможет определить цвет своего колпака.
10.7. Сначала сформулируем общую задачу.
По кругу сидят n мудрецов, они могут видеть и слушать друг друга. Им принесли n - 1 белый и n черных колпаков. Затем завязали глаза, надели всем черные колпаки, а белые спрятали. После этого мудрецам развязали глаза и стали поочередно спрашивать: "Знаешь ли ты цвет своего колпака?" Почти все ответили: "Не знаю", а последний сказал: "Знаю. Черный". Как он рассуждал?
Приведем рассуждения четвертого мудреца для n = 4. "Если на мне белый колпак, то остались два белых и четыре черных колпака. Но в таком случае третий мудрец смог бы определить, что у него черный колпак (для этого ему пришлось бы всего лишь решить предыдущую задачу). Раз он сказал, что не знает, на мне черный колпак".
Рассуждения последующих мудрецов аналогичны. Строгое решение задачи о мудрецах в общем виде можно изложить с помощью метода математической индукции.
10.8. Подсказка. Решите сначала задачу для одного мудреца, затем постепенно увеличивайте их количество.
Решение. 1) Если бы грязный мудрец был один, он вышел бы на первой станции.
Если грязных мудрецов двое, то на первой станции каждый понадеется, что грязный другой, поэтому никто не выйдет. После этого первый мудрец подумает: "Если бы я был чист, второй мудрец догадался бы, что он грязный, и вышел бы на первой станции. Но он не вышел, следовательно, я испачкался". Так же подумает и второй мудрец, и оба выйдут на второй станции.
Если грязных мудрецов трое, то на первых двух станциях никто не выйдет. А перед третьей третий мудрец подумает: "Если мое лицо чистое, то двое оставшихся мудрецов должны вести себя так, словно меня нет. Но в таком случае они вышли бы на второй станции. Раз они не вышли, мое лицо грязное". Так же подумают и два первых мудреца, и все трое выйдут на третьей станции.
Рассуждая аналогично, получаем, что все семь мудрецов выйдут на седьмой станции.
2) Снова начнем с простых случаев. Если мудрец один, то от проводника он узнал, что кто-то испачкался. Если мудрецов двое, то каждый и без проводника знал, что кто-то испачкался. Но из слов проводника он понял, что и другой знает, что кто-то испачкался.
Пусть мудрецов трое. Третий видел грязные лица первого и второго и понимал, что первый и второй знают, что кто-то испачкался. Но вот знает ли второй, что первый знает, что кто-то испачкался? Знает, но это стало известно третьему лишь после слов проводника. Это же можно сказать и о других мудрецах. Итак, все мудрецы узнали, что все знают, что все знают, что кто-то испачкался.
Рассуждая аналогично, добираемся до семи мудрецов. Из слов проводника все узнали, что все знают, что все знают, что все знают, что все знают, что все знают, что все знают, что кто-то испачкался. Заметим, что глагол "знать" повторяется столько же раз, сколько было мудрецов и станций.
10.9. "Среди вас есть испачкавшиеся" означает, что на ком-то надет черный колпак. Никто не сообщал это мудрецам словами. Но зато они видели, что белых колпаков на один меньше, чем мудрецов.
Комментарий. А если бы их было на два меньше? Тогда как минимум на двух мудрецах были бы черные колпаки. Это бы соответствовало словам проводника "Среди вас как минимум двое испачкались". В таком случае мудрецы бы вышли на одну станцию раньше (а в задаче про колпаки цвет своего колпака назвал бы предпоследний мудрец).
Заметим, что для полного соответствия задач следовало не спрашивать мудрецов поочередно, а всех мудрецов одновременно просить написать, знают ли они цвет своего колпака, а затем показывать записки друг другу.
10.10. Смех.
10.11. Приведем возможный пример.
1. Вор Карл украл кораллы.
2. Его друг Фридрих знает, что Карл украл кораллы (но не доносит).
3. Следователь Шерлок знает, что Фридрих знает, что Карл украл кораллы (и хочет арестовать Фридриха).
4. Клара знает, что Шерлок знает, что Фридрих знает, что Карл украл кораллы (и предупреждает Фридриха, что ему надо скрыться).
5. Шерлок знает, что Клара знает, что Шерлок знает, что Фридрих знает, что Карл украл кораллы (и хочет допросить Клару).
6. Клара знает, что Шерлок знает, что Клара знает, что Шерлок знает, что Фридрих знает, что Карл украл кораллы (и благополучно скрывается вместе с Фридрихом).
Дополнительные задачи
Д1. Если Саша мальчик, а Женя девочка, то оба ребенка говорят правду. Противоречие. Если Саша девочка, а Женя мальчик, то оба ребенка врут, что не исключается условием "хотя бы один из них врет".
Ответ. Саша – девочка, а Женя – мальчик.
Д2. Рассмотрим честного конгрессмена в паре со всеми остальными по очереди. По условию 2 второй в паре всегда продажен.
Ответ. Один.
ДЗ. 1) Легко видеть, что Ваня говорит правду (если предположить, что он лжет и высказывание "Я не всегда говорю правду" не является правдой, то правдой будет: "Я всегда говорю правду", т. е. получится противоречие).
2) Так как смысл высказывания Антона такой же, то Антон тоже говорит правду.
3) По условию, один из мальчиков солгал, значит, это – Саша.
4) Саша сказал: "Антон не всегда говорит правду" – и при этом солгал, значит, Антон всегда говорит правду.
Ответ: Антон.
Д4. В этом утверждении говорится об истинности его самого. Поэтому его нельзя считать не истинным, ни ложным, то есть оно вообще не является высказыванием.
Комментарий. Рассмотрим такое решение. "Если это высказывание истинно, т. е. правил без исключения нет, то и из этого правила есть исключения, и правила без исключения все-таки есть. Пришли к противоречию. Значит, высказывание ложно, и существует хотя бы одно правило без исключения (хотя и не это)". Ошибка выходит на поверхность, если представить, что это правило единственное. И тогда правилу без исключения взяться неоткуда. Если же заранее договориться, что существуют хотя бы два правила, то эту фразу можно считать ложным высказыванием. Аналогично, если считать, что на Крите есть хотя бы два жителя, и только один из них сказал "Все критяне лжецы", парадокс Эпименида перестает быть парадоксом.
Д5. 1) Не каждый охотник желает знать, где сидит фазан. 2) Существует хотя бы один охотник, не желающий знать, где сидит фазан. 3) Некоторые охотники не желают знать, где сидит фазан.
Д6. Все лжецами быть не могли (в таком случае сказанное каждым оказалось бы правдой), был хотя бы один рыцарь. Он сказал правду, поэтому все остальные были лжецами.
Ответ. Один.
Д7. Первое можно опровергнуть контрпримером (начертив прямоугольник с неравными сторонами), третье и четвертое доказать примером (начертив любой квадрат), а доказать второе помогут определения прямоугольника и квадрата.
Ответ. Первое утверждение ложно, а остальные истинны.
Д8. 1) Некоторые друзья моего друга не являются моими друзьями. 2) Некоторые ананасы приятны на вкус. 3) Ни один волк не является оборотнем.
Д9. Чтобы разобраться в трех замысловатых условиях, удобно для начала перечислить все возможные виды зоопарков с точки зрения наличия жирафов, носорогов и гиппопотамов. Их всего восемь:
1) ЖНГ; 2) ЖНГ; 3) ЖНГ; 4) ЖНГ;
5) ЖНГ; 6) ЖНГ; 7) ЖНГ; 8) ЖНГ.
Здесь запись ЖНГ, например, означает, что в зоопарке есть жирафы, нет носорогов и есть гиппопотамы. В силу первого условия вычеркиваем зоопарки вида 1, в силу второго – вида 7, в силу третьего – вида 2. Теперь видно, что ничто не противоречит существованию зоопарков вида 6.
Эти рассуждения могут быть изображены с помощью кругов Эйлера. Области на рис. 30 пронумерованы в соответствии с приведенным списком. Зоопарки, запрещенные условием, закрашены серым. Зоопарки, соответствующие остальным областям, могут существовать, в том числе и соответствующие шестой области.
Ответ. Да.
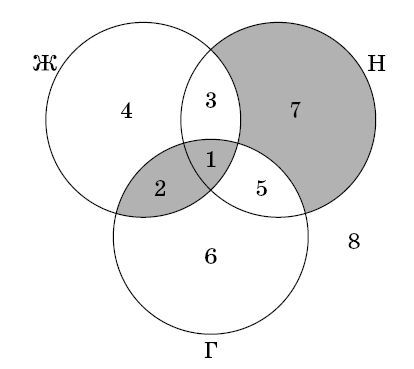
Рис. 30
Д10. Чтобы выполнить пожелание Ани, необходимы и яблоки, и сливы. Чтобы порадовать Галю, нужны еще и персики. Остается лишь проверить, что Боря и Витя при этом тоже будут довольны.
Ответ. Надо купить яблоки, сливы и персики.
Д11. 1) Луна сделана не из сыра или Солнце не из масла.
2) Я не видел медведя или он видел меня.
3) Я боюсь львов или крокодилов.
4) Лошадь не заблудилась и ее не засыпало снегом.
5) Я не отправился в разведку ни на коне, ни на ядре.
Д12. Третья дверь может вести только в учительскую. Значит, за дверью с табличкой "Спортзал" не спортзал и не учительская, т. е. столовая.
Ответ. В столовую.
Д13. Если Руссо прав, то Жан и Жак оба лгут, чего не может быть (вспомните, что говорит Жан). Значит, Руссо лжет. Поэтому Жак прав. А тогда Жан лжет.
Ответ. Правду говорит только Жак.
Д14. Если А – рыцарь, то ОБЕ части его высказывания правдивы. Но в одной из них сказано, что он лжец. Противоречие. Значит, А – лжец. Первая часть его высказывания истинна, поэтому ложной должна быть вторая часть (тогда и все высказывание ложно). Поэтому Б тоже лжец.
Ответ. Оба лжецы.
Д15. Решение 1. Все трое рыцарями быть не могли (в таком случае они не стали бы называть друг друга лжецами).
Два рыцаря и один лжец тоже быть не могли (в таком случае оба утверждения ложны, а лжец только один).
Два лжеца быть могли. Например, Ох и Ух, которые и сделали ложные утверждения, так как Ах – рыцарь.
Все трое лжецами быть не могли, так как в таком случае оба утверждения истинны.
Решение 2. Если оба ответа ложны, то среди троих двое солгали и есть хотя бы один рыцарь, то есть лжецов ровно двое. Если же среди ответов есть верный, то его дал рыцарь, а двое им названных – лжецы. Пример: рыцарь Ух сказал, что Ах и Ох лжецы.
Ответ. Двое.
Д16. Если бы А был лжецом, его высказывание оказалось бы истинным. Поэтому он рыцарь. В таком случае он говорит правду, и Б – лжец.
Комментарий. Задача напоминает парадокс лжеца: здесь также сказанное имеет отношение к его истинности. Но наличие второго островитянина Б превращает парадокс в задачу с однозначным ответом.
Д17. Среди них нет рыцарей, и оба они не могут быть лжецами, потому что тогда они бы сказали правду. Значит, либо оба они хитрецы, либо один хитрец, а другой лжец.
Д18. Решение 1. Посмотрим, кто может быть рыцарем. Это не А, называющий себя хитрецом. И не Б, так как в этом случае никто не мог бы быть лжецом. Значит, рыцарь – В. Он говорит правду, поэтому Б – хитрец. Тогда А – лжец. Заметим, что высказывание хитреца Б ложно.
Решение 2. Предположим, что А сказал правду и он действительно хитрец, тогда В солгал и он лжец. В этом случае Б должен быть рыцарем. Но его высказывание неверно, так как В никогда не говорит правду. Получили противоречие. Предположим теперь, что А солгал, тогда он лжец, и, следовательно, высказывание Б ложно. Значит, Б – солгавший хитрец, а В – рыцарь, что подтверждается его верным высказыванием.
Ответ. А – лжец, Б – хитрец, В – рыцарь.
Д19. Высказывания Ромы и Коли противоположны, поэтому истинно ровно одно из них. Это же можно сказать о высказываниях Маши и Нины. Кроме того, из высказывания Саши следует, что либо он говорит правду, либо Аня. Значит, из высказываний Ани и Саши истинно тоже ровно одно. Поскольку истинных высказываний ровно три, оставшиеся высказывания (Володи, Егора и Олега) ложные. Окно разбила Нина.
Ответ. Нина.
Д20. В понедельник, вторник, среду, пятницу и воскресенье.
Д21. Если в думе есть хоть один рыцарь, то всего в ней четное число депутатов, и спикер – лжец. А если нет ни одного рыцаря, то он тем более лжец!
Ответ. Лжец.
Д22. Формально: см. третью строку таблицы истинности высказывания "А ⇒ Б". Неформально: у волка есть и другие причины для радости.
Ответ. Нет.
Д23. Достаточно привести любой пример, в котором все три высказывания верны, но Иван не является братом Марьи. Иван может приходиться Марье отцом, дядей, племянником и т. д.
Ответ. Нет.
Комментарий. К ошибочному выводу можно было бы прийти, перепутав в первом высказывании причину и следствие и ошибочно заменив его на обратное: "Если Иван и Марья – родственники, то Иван – брат или сын Марьи".
Д24. Если этот житель рыцарь, то он сказал правду, и его друг действительно лжец. А если он сам лжец? Тогда любое утверждение, начинающееся со слов "Если я рыцарь…" оказывается истинным и просто не может быть произнесено лжецом!
Ответ. Да; он – рыцарь, а его друг лжец.
Д25. Если у Волкова нет собаки, то ее нет и у Львова, тогда собаку держит Щукин. В таком случае у Волкова кошка, а у Львова рыбки. Но по последнему условию если у Львова рыбки, то у Щукина кошка. Полученное противоречие показывает, что у Волкова есть собака. Если бы кошка жила у Щукина, то у Волкова был бы аквариум. Значит, кошку держит Львов, а рыбок – Щукин.
Ответ. У Львова кошка, у Волкова собака, а у Щукина рыбки.
Д26. Из третьего и четвертого условий Нуф-Нуф и Наф-Наф либо оба виновны, либо оба невиновны. Поэтому по второму условию Ниф-Ниф невиновен. Поэтому и Нуф-Нуф с Наф-Нафом невиновны (из пятого условия). Итак, никто челюсть украсть не мог, а обвинение в лжесвидетельстве Шерлок Холмс предъявит Серому волку.
Д27. Иа-Иа не мог участвовать в краже одновременно с Тигрой (так как им требуется различное число соучастников). Поэтому если Тигра виновен, то вместе с ним был либо Пятачок (а тогда и Винни-Пух), либо только Винни-
Пух. Если виновен Иа-Иа, то два его соучастника – Пятачок и Винни-Пух. А если ни Тигра, ни Иа-Иа ни при чем, то мед украл либо Пятачок (а тогда он был вместе с Винни-Пухом), либо только Винни-Пух.
Ответ. Винни-Пуха.
Д28. 1) Приведем контрпример: -5; 2; 2; 2; -5; 2; 2; 2; -5.
Ответ. Нет.
2) Возьмем произвольные четыре числа. Их сумма положительна, поэтому положительно хотя бы одно из этих чисел. Возьмем его, а остальные восемь чисел разобьем на две четверки чисел, сумма которых положительна.
Ответ. Да.
Комментарий. Для обоснования отрицательного ответа в первом случае достаточно одного контрпримера. Для обоснования положительного ответа во втором случае необходимо доказательство.
Д29. 1) Ложно. Можно сделать лишь вывод о том, что некоторые улитки любят кошек.
2) Истинно.
Д30. 1) Устрица не является ископаемым животным.
2) Со мной никогда не случалось этого.
3) Вывод сделать нельзя.
4) Дети не управляют крокодилами.
5) Ни один из твоих подарков не сделан из олова.
Д31. Из условия следуют только два утверждения – второе и четвертое.
Д32. Это задача-шутка. Первый вывод в бытовой речи допустим, хотя автор "Мертвых душ" – не единственный носитель фамилии Гоголь, и нельзя исключать наличие портрета другого Гоголя. Второй вывод явно неверен. Отличие в употреблении неопределенного местоимения "какой-то". Фразам с неопределенными местоимениями в логике соответствуют не высказывания, а предикаты; их серьезное изучение выходит за рамки данной книжки.
Д33. Если бы такое число существовало, то вдвое меньшее число тоже было бы рациональным и положительным.
Ответ. Нет.
Д34. Предположим, что заработок Папы Карло каждый месяц был целым. Перечислим месяцы в порядке возрастания заработка. Тогда за первый месяц Папа Карло заработал не менее нуля золотых, за второй не менее одного…, за двенадцатый не менее одиннадцати. Всего он заработал не менее 0 + 1 + 2 +.. + 11 = 66 золотых, что противоречит условию. Значит, предположение неверно, и какой-то из заработков не был целым.
Д35. На круге чередуются группы подряд идущих четных чисел с группами подряд идущих нечетных. Предположим, что нет двух четных чисел рядом. Если в каждой "четной" группе – ровно одно число, то таких групп 1005. Значит, и "нечетных" групп 1005, то есть столько, сколько нечетных чисел. Тогда и в каждой "нечетной" группе – по одному числу, то есть четные и нечетные числа строго чередуются. Но это значит, что либо каждое четное число больше обоих соседних нечетных, либо каждое четное число меньше обоих соседних нечетных. В первом случае не найдется места для числа 2, а во втором – для числа 2010. Противоречие.