Первыми сотрудниками стали преимущественно бывшие московские студенты Яблонского и самого Ляпунова. Новая кафедра быстро приобрела статус центра кибернетических исследований – второго по значимости в Советском Союзе. Почти сразу к исследовательскому коллективу присоединился Борис Трахтенброт, который также занимался кибернетикой и на тот момент – в сорок с небольшим лет – уже был доктором наук; вскоре Трахтенброт стал одним из ведущих сотрудников кафедры. В 1962 году в Новосибирск приехал Ян Мартынович Барздинь, незадолго до того защитивший кандидатскую в Латвийском государственном университете в Риге. Трахтенброт и Барздинь начали совместные исследования в области сложности вычислений и привлекли к работе множество российских и латышских студентов. В середине шестидесятых ученые уже вовсю разрабатывали теорию алгоритмической сложности – аналогичную той, что в то же самое время создавалась на Западе.
Впрочем, в СССР с вычислительной сложностью все было довольно сложно. В 1984 году Трахтенброт напишет:
"Напряженность в отношениях с представителями так называемой классической школы – и в особенности с Яблонским – нас очень угнетала. Эти люди занимали крайне негативную позицию касательно применения теории алгоритмов к вопросам сложности <…> Они не допускали и мысли о том, что вычислительную и алгоритмическую сложность можно связать с проблемой перебора. Яблонский к тому времени играл уже далеко не последнюю роль в различных организациях, занимавшихся планированием и контролем математических исследований; в дальнейшем наше противостояние только усилилось – по всей видимости, из-за разногласий по поводу необходимости перебора".
Летом 1963 года в Новосибирск приехал Колмогоров и начал совместные исследования с Трахтенбротом. Ученые пытались понять, каким образом теория алгоритмов может помочь им продвинуться в изучении сложности и информации.
Из Новосибирска Колмогоров вскоре отправился в Киев, где посетил физико-математическую школу-интернат при Киевском университете. Ученый предложил школьникам несколько задач; пятнадцатилетний Леонид Левин справился почти со всеми. Позже Колмогоров пригласил его в Московский университет и взял под свое руководство. Во время учебы в аспирантуре Левин разрабатывал сразу два разных направления.
В рамках одного из них был создан оптимальный алгоритм поиска. Допустим, Элис говорит Бобу, что придумала быстрый алгоритм для задачи о клике, но отказывается его показать. Применив метод Левина, Боб сможет сам создать почти такой же быстрый алгоритм – и для этого ему не нужно будет знать, что написала Элис. В работе Левина используется модифицированный вариант колмогоровской сложности; его оптимальный алгоритм особым образом запускает все возможные алгоритмы, проверяя, дают ли они нужное решение.
Размышляя о задачах поиска и проблеме перебора, Левин пришел к понятию универсальной переборной задачи, которое было эквивалентно понятию NP-полной задачи, введенному Куком. Ученый рассмотрел шесть переборных задач, включая выполнимость, и показал их универсальность, а также сформулировал проблему равенства классов P и NP.
Блестящие результаты! И второй, безусловно, достоин награды; Стивен Кук за аналогичные достижения получил премию Тьюринга. Колмогоров, однако, счел работы Левина несколько сырыми и настоял на том, чтобы вместе довести их "до кондиции". В те годы в Советском Союзе было принято сокращать публикуемые статьи, опуская подробности доказательств. Следуя этому правилу, Левин сократил текст по максимуму и уместил все свои исследования в каких-то две страницы.
Вскоре Левин представил кандидатскую диссертацию; предыдущие работы он в нее включать не стал. Вся советская молодежь тогда состояла в комсомоле – молодежной организации Коммунистической партии. Независимый и свободомыслящий Левин открыто саботировал комсомольские мероприятия, не осознавая, вероятно, к чему это может привести. В конце концов его диссертацию не приняли по причине "неопределенности политического облика".
Политическая травля Левина не прекращалась. В 1978 году ему удалось эмигрировать в Соединенные Штаты. Альберт Мейер из Массачусетского технологического института стал его научным руководителем; спустя год Левину присудили степень доктора философии – за выдающиеся результаты, полученные еще в Советском Союзе. В настоящее время Левин – профессор Бостонского университета.
В Соединенных Штатах об исследованиях Левина узнали в середине семидесятых, когда проблема равенства P и NP уже широко обсуждалась в научных кругах. Левину не пришлось разделить с Куком премию Тьюринга, которую тот получил в 1982 году; и все-таки основной результат касательно NP-полноты со временем стали называть теоремой Кука–Левина – правда, произошло это уже ближе к девяностым.
Потепление в отношениях между СССР и США началось в 1980-х. В седьмой главе мы поговорим о попытках разработать методы для доказательства неравенства P и NP, опирающиеся на теорию сложности схем; ведущую роль в этих разработках сыграл советский и российский математик Александр Разборов, бывший в ту пору студентом.
После распада Советского Союза пришел конец и вынужденной изоляции ученых. А с развитием интернета весь мир превратился в единое научно-исследовательское сообщество.
Письмо Гёделя
В 1956 году Курт Гёдель написал письмо Джону фон Нейману – пионеру в информатике и многих других областях науки. В письме Гёдель на немецком языке рассуждал о проблеме выполнимости и о вопросе равенства классов P и NP, только формулировал он этот вопрос в несколько иных терминах. По словам ученого, если бы мы жили в мире, в котором P = NP, то "математикам более не пришлось бы тратить время на задачи типа "да-нет": этот труд за них выполняли бы машины <…> Впрочем, я уже перестал относить эту возможность к области несбыточного". Идеи Гёделя на пятнадцать лет опередили работы Левина и Кука.
Получил ли фон Нейман то письмо? Ответил ли он Гёделю? Мы этого не знаем; на тот момент фон Нейман уже был болен раком, и в 1957 году его не стало. О письме научное сообщество узнало лишь в конце восьмидесятых, когда за вопросом о равенстве P и NP уже прочно закрепился статус одной из центральных открытых научных проблем. Сам Гёдель умер в 1978 году; душевное расстройство, омрачившее последние годы его жизни, помешало ученому понять, что Кук в своей работе поднял тот же вопрос.
Так почему бы не назвать вопрос "проблемой Гёделя"? Почему не признать за Гёделем приоритет? Ведь он пришел к нему намного раньше, чем Кук и Левин! К сожалению, – или, возможно, к счастью, – в науке действует тот же принцип, что и в мореплавании: Христофор Колумб прославился не потому, что первым открыл Америку, а потому, что открыл ее последним. Впрочем, Гёдель тут и сам, как говорится, дал маху: не осознавая значимость поднятых в письме к фон Нейману вопросов, ученый никогда не публиковал свои идеи. Если смотреть на публикации, то первыми проблему равенства P и NP сформулировали все-таки Кук и Левин.
В 1993 году научное сообщество, отдавая дань Гёделю за его фундаментальный вклад в логику и высказанные в письме идеи, учредило премию в его честь. Премией Гёделя отмечают недавно появившиеся работы в области теоретической информатики.
Правило марсианина
Как узнать, какое понятие в науке – естественное, подсказанное самой природой, а какое – искусственный продукт деятельности человеческого разума? Представьте, что на Марсе обнаружили цивилизацию, которая находится примерно на таком же уровне развития, что и наша. Если для некоторого земного понятия существует марсианский аналог, полностью идентичный или хотя бы схожий по смыслу, значит, это понятие естественное, поскольку происходит из двух независимых источников.
Понятно, что цивилизации на Марсе нет и сравнивать нам там себя на самом деле не с кем, но мы ведь можем подключить воображение! Допустим, у марсиан имеется машина Экзигия – вычислительная модель, отличная от машины Тьюринга, но обладающая абсолютно теми же возможностями. Марсианский вариант тезиса Чёрча – Тьюринга гласит: все, что можно вычислить, вычислимо и на машине Экзигия. Значит, понятие вычислимости естественно, а вот понятие машины Тьюринга – нет.
В случае с классами P и NP можно обойтись без марсиан. Советские и американские математики практически не имели возможности общаться; они параллельно проделали одну и ту же работу и независимо сформулировали проблему равенства P и NP и понятие NP-полноты. Мотивы были разными: на Западе разбирались с вычислительной эффективностью, на Востоке – с необходимостью перебора; в результате обе стороны пришли туда же, куда и Курт Гёдель, опередивший их на пятнадцать лет.
Точно так же и марсиане – если бы они, конечно, существовали – могли бы прийти к проблеме равенства P и NP или чему-то подобному и отнести ее к разряду важных и естественных.
Глава 6. Преодолевая трудности
Во второй главе мы с вами побывали в идеальном мире. Равенство P и NP сделало нашу жизнь прекрасной и удивительной. Исследовать можно было все. Оптимизировать – тоже. Машины умели выполнять почти все мыслимые и немыслимые операции. Прекрасно, волшебно, пугающе… и, скорее всего, нереально.
На самом деле мир наверняка далек от совершенства – этакая "неэлегантная вселенная", в которой P и NP не равны. Во всяком случае, именно в таком мире мы будем жить до тех пор, пока не найдем эффективный алгоритм для решения задач из NP. Но что же делать, если мы не можем эффективно решить какую-то задачу? Оставить на потом?
К сожалению, некоторые трудные задачи нельзя так просто взять и отмести. Гарри работает планировщиком на производственном предприятии "Рога и копыта". Его босс Эми поручает ему настроить линию на сборку последней модели мобильного телефона "Эйфон" и минимизировать при этом время сборки. Гарри читал предыдущие главы нашей книги, поэтому смело отвечает: "Извините, но эта задача NP-полная. Если даже известные ученые считают, что быстрого решения нет, то что уж мне пытаться? Я лучше в боулинг пойду поиграю". На что Эми разрешает ему веселиться хоть до утра, поскольку в "Рогах и копытах" он больше не работает.
На место Гарри в срочном порядке наняли Джорджа. К счастью для себя, Джордж читал эту главу и потому сумел настроить линию на производство "Эйфонов". Неужели он изобрел гениальный алгоритм, который всегда оптимально распределяет подзадачи? Нет. Но с работой он все-таки справился? Безусловно.
NP-полные задачи "приручить" не так-то просто. Если P ≠ NP, то мы никогда и ни для одной из них не найдем хороший, быстрый алгоритм, который бы во всех случаях выдавал наилучшее решение. Впрочем, это вовсе не значит, что сделать ничего нельзя. В данной главе мы рассмотрим несколько подходов к решению трудных задач.
Современные процессоры настолько мощны, что, когда размер входа не очень велик, можно просто перебрать все потенциальные решения. Также можно применять алгоритмы, которые не годятся для некоторых частных случаев, однако по большей части работают вполне приемлемо. Кроме того, существуют алгоритмы, которые выдают пусть и не оптимальное, но все же довольно близкое к нему решение.
Иногда NP-полная задача упорно не желает поддаваться. Что с ней делать? Перейти к другой NP-полной задаче. Или взять и плюнуть на все, потому что есть дела и поважнее.
Полный перебор
Современные компьютеры считают очень быстро. Невероятно быстро. С невообразимой, умопомрачительной скоростью. Даже ноутбук или планшет может выполнить полный перебор потенциальных решений для задачи с небольшим размером входа.
Однако раньше все было совсем по-другому. В 1971 году, когда Стивен Кук поднял вопрос о равенстве P и NP, компания Intel выпустила микропроцессор Intel 4004 – первый полноценный центральный процессор, который уместился на одном кристалле и стал доступным для потребителей. Intel 4004 мог выполнять 92000 операций в секунду и для того времени был очень скоростным.
Возьмем для примера подробно разобранную Куком задачу о выполнимости и рассмотрим случай с двадцатью переменными. Применим к ней простейший алгоритм, который методично перебирает все возможные комбинации значений переменных, устанавливая их в TRUE или FALSE. Если предположить, что на обработку одной комбинации уходит 100 шагов, то выполнимость всей формулы будет проверяться примерно 19 минут. Долго, конечно, но ведь могло быть и хуже! Однако проблема в том, что с двадцатью переменными каши особо не сваришь.
Двадцать пять переменных обрабатывались бы примерно 10 часов. Тридцать – чуть больше 13 суток. Ну а с сорока переменными мы бы ждали с 1971-го года по 2009-й.
Сейчас Intel каждый год выпускает несколько новых моделей процессоров. Рассмотрим, к примеру, появившийся в 2009-м Intel i7–870, который мог выполнять 2,93 миллиарда операций в секунду – в 30000 раз больше, чем Intel 4004. С сорока переменными он справился бы часов за десять, так что в 1971-м быстрее было бы просто подождать 38 лет и воспользоваться технологиями 2009-го.
Для некоторых NP-полных задач можно привести и более впечатляющие примеры. Возьмем задачу о коммивояжере, который ищет кратчайший маршрут, проходящий через максимально возможное число городов. Применяя метод секущих плоскостей, мы легко найдем решение даже для 10000 городов. На рисунке ниже представлено решение для 13509 населенных пунктов с населением от 500 человек.
Впрочем, обычно потенциальных вариантов бывает слишком много; не стоит и надеяться решить даже среднюю по размеру задачу.
Современные микросхемы работают почти на пределе физических возможностей. Впрочем, число транзисторов на одном кристалле неизменно увеличивается, так что производительность компьютеров пока продолжает расти с той же бешеной скоростью, подтверждая закон Мура. Когда-нибудь мы наверняка научимся решать NP-полные задачи гораздо большего размера. Однако при увеличении размера входа трудоемкость задачи также сильно возрастает, поэтому не стоит ждать, что уже в ближайшем будущем мы сможем быстро проверять выполнимость для 150 переменных или находить коммивояжеру оптимальный маршрут на 20000 городов.
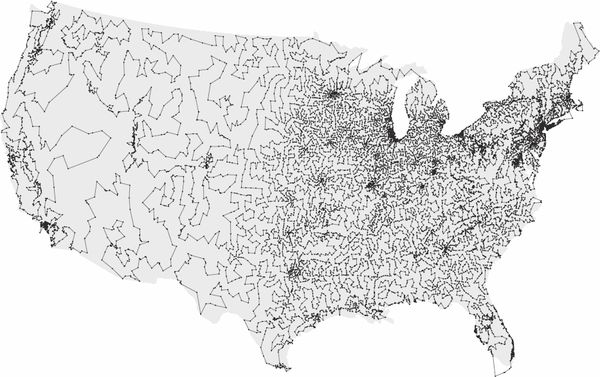
Рис. 6.1. Коммивояжер: города с населением более 500 человек
Эвристические методы
Когда английскому плотнику XVII века требовалось прикинуть расстояние в дюймах, он ориентировался на ширину своего большого пальца. Вероятно, отсюда и пошло так называемое правило большого пальца – простой и неточный, но вполне приемлемый метод решения того или иного вопроса. К примеру, поговорка "Красный закат – моряк, веселись! Красный рассвет – моряк, берегись!" дает нам примитивный, но достаточно надежный метод предсказания погоды. А закон Мура грубо оценивает рост мощности компьютеров.
Любой вычислительный алгоритм – это тоже метод решения какого-либо вопроса. Эвристические алгоритмы работают подобно правилу большого пальца: иногда они ошибаются, однако в большинстве случаев находят верное решение. Для NP-полных задач такие алгоритмы начали появляться задолго до того, как об их NP-полноте стало известно. За последние десятилетия сложными эвристическими методами "обзавелось" огромное множество трудоемких задач. Ни один из этих методов не является универсальным и не годится для всех случаев сразу, однако в общем и целом они со своей работой справляются.
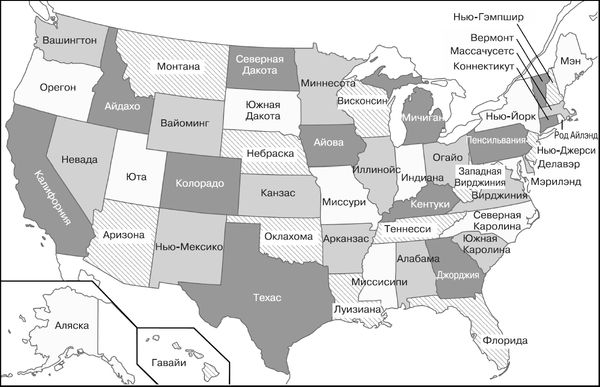
Рис. 6.2. Карта Соединенных Штатов
Давайте подробно рассмотрим простой, но очень мощный эвристический алгоритм раскраски карт. В третьей главе мы объяснили, почему для правильной раскраски карты Соединенных Штатов, т. е. для раскраски, при которой соседние штаты имеют разные цвета, требуется не меньше четырех цветов.
Неваду окружает кольцо из пяти штатов: Калифорния, Орегон, Айдахо, Юта и Аризона. Для раскраски всех штатов кольца требуется не меньше трех цветов; Невада имеет с ними общие границы, так что для нее придется добавить четвертый. Другие штаты также образуют подобные кольца: к примеру, штат Кентукки окружают Теннесси, Вирджиния, Западная Вирджиния, Огайо, Индиана, Иллинойс и Миссури. Здесь нам тоже, как и в случае с Невадой, понадобится три цвета для кольца и четвертый для Кентукки.
Любую карту, на которой есть хотя бы один регион, окруженный нечетным количеством других регионов, невозможно раскрасить меньше чем в четыре цвета.
На рисунке ниже представлена карта областей Армении.
Всего две из них целиком лежат внутри страны. Котайк окружен шестью областями, а столица Ереван – четырьмя. Эвристический метод говорит нам, что если все внутренние регионы имеют четное число соседей, то для раскраски карты хватит трех цветов. И мы видим, что для Армении так и получается.
Швейцарию окружает нечетное число соседей – пять. Это Франция, Италия, Австрия, Лихтенштейн и Германия. Несмотря на это, карту на рис. 6.5 тоже можно раскрасить в три цвета.
Дело в том, что Лихтенштейн вклинился между Швейцарией и Австрией и разбил их общую границу на две, поэтому Австрию нужно учитывать дважды. Оказывается, важно не количество соседних государств, а количество общих границ; у Швейцарии их шесть, а шесть – число четное. Заметим, что считаются только внешние границы, и страны, целиком лежащие внутри другого государства, не учитываются вообще (например, Ватикан внутри Италии).
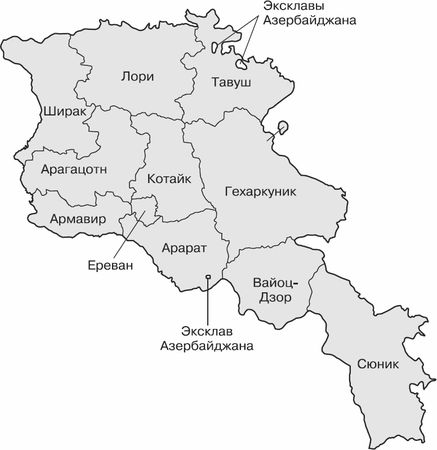
Рис. 6.3. Армения
Если бы наш эвристический метод всегда выдавал верное решение, это означало бы, что для раскраски в три цвета существует эффективный алгоритм, а поскольку задача раскраски NP-полна, то и для всех остальных NP-задач тоже существует эффективный алгоритм, поэтому P = NP. Думаю, вы уже догадались, что иногда у него случаются проколы?
Эвристический метод имеет ровно два исключения.
1. На карте имеется озеро, по которому проходит граница между регионами. Например, озеро Мичиган отделяет Иллинойс от штата Мичиган.