Разбиение генома по биологическим функциям: универсальный степенной закон
До сих пор в нашем обсуждении универсальных количественных закономерностей в геномной эволюции мы преднамеренно обходили стороной вопрос биологических функций. Конечно, это абстракция: геном ни в коем случае не сумма безликих "молекул", а ансамбль генов, каждый из которых кодирует определенную биологическую функцию. Сначала может показаться неожиданным, что способ рассуждения, позаимствованный из статистической физики, может быть применен и к биологическим функциям. Для применения такого подхода необходимо разделить гены на большие функциональные классы, о которых можно думать как о разных типах "молекул" и которые пригодны для статистического анализа, если они включают достаточно много генов.
Как показывается в серии доскональных исследований Эрика Ван Нимвегена, различные функциональные классы генов по-разному соотносятся с общим числом генов в геноме (Molina and van Nimwegen, 2009; van Nimwegen, 2003). Не учитывая некоторые отклонения, для прокариот можно указать три основных показателя степени, описывающие эти соотношения: 0, 1 и 2. Генам белков, участвующих в информационных процессах (трансляции, транскрипции и репликации), соответствует показатель степени 0 – число таких генов достигает некоторого константного значения уже в минимальных геномах и в принципе не зависит от сложности генома. Число метаболических ферментов и транспортных белков примерно прямо пропорционально общему числу генов (показатель степени 1). Регуляторные гены и компоненты систем передачи сигналов показывают квадратичную зависимость (показатель степени равен 2; рис. 4-10). Показатели степени этих трех обширных классов остаются неизменными, с очень небольшими отклонениями, для всех групп прокариот, и это позволяет предположить, что разница в эволюционной динамике генов с различными функциями отражает какие-то фундаментальные законы эволюции клеточных организмов, или, другими словами, строгие и четко выраженные ограничения в функциональном устройстве геномов. Для генов эукариот обнаружены похожие, хотя и не такие явные, степенные соотношения, показатель степени для регуляторных генов эукариот значительно больше 1 (хотя и меньше 2). Имея в виду все вышесказанное, можно заключить, что эти соотношения представляют еще один набор универсалий геномной эволюции, которые становятся еще интереснее при рассмотрении их связи с функциональным устройством клетки.
Фундаментальные причины существования различных соотношений для различных функциональных классов генов еще не выяснены. Привлекательно простая модель эволюции метаболических сетей прокариот как "ящика с инструментами", предложенная Сергеем Масловым и коллегами, может быть первым шагом на пути объяснения квадратичной зависимости, характерной для регуляторных генов (Maslov et al., 2009). В этой модели ферменты, необходимые для утилизации новых метаболитов, добавляются вместе с соответствующими им регуляторами (в первую очередь посредством горизонтального переноса генов, гл. 5) во все более развитую сеть реакций. В результате усложнения сети, обеспечивающей все большее разнообразие ферментов промежуточных реакций, увеличивается отношение числа регуляторных генов к регулируемым. В какой-то момент, и его наступление можно точно предсказать, цена добавления новых регуляторов неизбежно станет слишком невыгодной ("разрастающаяся бюрократия") и будет ограничивать рост сложности генома.
Гипотеза "бюрократического потолка" для верхней границы сложности генома выглядит особенно правдоподобно в свете почти полного отсутствия роста числа генов в геномах позвоночных, особенно млекопитающих (и в наших геномах тоже), для которых связь между числом генов и размером генома очевидно нарушена (см. гл. 3 и 8). В принципе число генов могло бы быть напрямую ограничено ценой репликации ДНК, но для огромных геномов позвоночных этот фактор можно смело исключить как главное ограничение. Соответственно, цена регуляции, возможно совместно с ценой экспрессии, выглядит наиболее вероятным кандидатом на роль основного фактора, ограничивающего рост числа генов. Поэтому не случайно позвоночные (и в меньшей степени другие многоклеточные эукариоты) выработали новые, замысловатые способы увеличения сложности протеома, такие как широко распространенный альтернативный сплайсинг, альтернативная трансляция и сложная регуляция (в особенности обширный, все еще слабо изученный набор регуляторных РНК). Такие формы сложности не вызывают инфляционный рост числа белок-кодирующих генов и, таким образом, снижают по крайней мере некоторые издержки, особенно издержки трансляции (см. гл. 8).
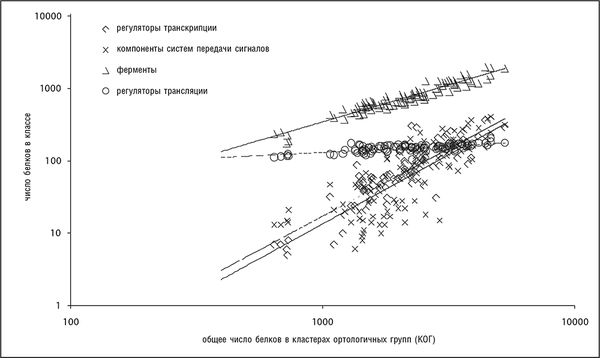
Рис. 4-10. Четко различающиеся соотношения между различными функциональными классами генов и размером генома (общим числом белок-кодирующих генов) прокариот. Использована информация из базы данных COG (Tatusov et al., 2003). График построен в двойных логарифмических координатах.
Универсальная зависимость численности функциональных классов генов от размера генома находится в обратной зависимости с ранее описанным степенным законом распределения численности семейств генов. Чем больше положительный показатель степени функции зависимости от размера генома для функционального класса генов (рис. 4-10), тем меньше отрицательный показатель степени функции распределения численности семейств в этом классе (рис. 4–7). Кажется интуитивно правдоподобным, что функциональные классы с сильной зависимостью от размера генома должны содержать много больших семейств паралогичных генов. Обратная зависимость этих двух универсалий генома была выведена в рамках простой эволюционной модели, в которой используются правила пропорциональных вычислений для функциональной композиции генома, например "добавить два регулятора на каждый метаболический фермент" (Grilli et al., 2011). Предсказания этой модели подтверждаются эмпирическими данными для многих геномов бактерий и архей.
Стохастичность, нейтральность и отбор в эволюции
В предыдущих разделах этой главы мы ознакомились со многими количественными универсалиями, отражающими важнейшие аспекты эволюции и функционирования генома. Среди этих универсалий мы рассматривали вездесущий степенной закон распределения, который описывает как структуру всех биологических сетей, так и семейства паралогичных генов в разнообразных геномах, близкое к логарифмически нормальному распределение скоростей эволюции генов и универсальные корреляции, такие как отрицательная корреляция между генной экспрессией и скоростью эволюции. Какова природа этих универсалий? Отражают ли они какие-то глубокие свойства эволюции или это просто статистические эффекты, не имеющие отношения к пониманию биологических явлений? Здесь и далее в этой книге (гл. 13) будет отстаиваться точка зрения на эти универсалии как на нетривиальные, характерные и биологически значимые тенденции, хотя они отражают только одну из двух (а возможно, и большего числа) дополнительных (в смысле принципа дополнительности Бора) составляющих эволюции жизни.
Во-первых, как это уже отмечалось и теперь совершенно очевидно, все эти универсалии зависимы от поведения совокупностей генов, фундаментальных единиц эволюции, рассматриваемых как статистические ансамбли. Таким образом, эти универсальные зависимости и распределения являются эмергентными свойствами биологических систем, то есть свойствами, проявляющимися в результате того, что эти системы состоят из многочисленных (достаточно многочисленных для проявления устойчивых статистических закономерностей) элементов (генов или белков, в зависимости от контекста), слабо взаимодействующих друг с другом (если сравнивать эти взаимодействия с теми, которые поддерживают целостность самих этих элементов).
Во-вторых, как мы уже видели, современный эволюционный анализ не останавливается на демонстрации существования универсальных понятий и законов. По крайней мере некоторые ключевые универсалии, такие как распределение эволюционных скоростей, отрицательные корреляции между скоростью эволюции и экспрессией и распределение численности паралогичных семейств, были теоретически выведены в рамках простых, но достаточно детализированных, формальных моделей эволюции. Способность простых моделей, в которых в качестве элементарных событий рассматриваются наиболее общие эволюционные процессы (такие как дупликация и утрата генов), объяснять геномные универсалии убеждает в том, что эти универсалии отражают существенные черты эволюции.
Третье, и, возможно, наиболее важное, замечание о новой парадигме понимания эволюции, которую мы пытаемся здесь обрисовать, состоит в том, что порождающие модели для общегеномных универсалий либо совсем не используют понятие отбора, либо используют только понятие очищающего (стабилизирующего) отбора. Эта форма отбора направлена на сохранение статуса-кво и наблюдается для укладки белковых молекул, для распределения численности генных семейств и для универсальной зависимости численности функциональных классов генов от общего числа генов (Koonin and Wolf, 2010b).
Аналогия между эволюционным процессом и статистической физикой не ограничена существованием универсальных зависимостей и распределений, некоторые из которых могут быть выведены в рамках простых моделей. Возможно также составить схему детального соответствия ключевых параметров этих двух областей (Barton and Coe, 2009; Sella and Hirsh, 2005). Такой параметр состояния (степень свободы), как положение частицы, в этой схеме является аналогом либо состояния сайта в нуклеотидной или белковой последовательности, либо состояния гена в геноме (в зависимости от уровня моделирования эволюции), и тогда параметрам скорости эволюции для сайта или гена будет соответствовать скорость частицы. Более того, значение эффективной численности популяции будет очевидно аналогичным значению температуры в статистической физике, а приспособленность будет соответствовать свободной энергии.
Краткий обзор и перспектива: о природе эволюционного процесса
Результаты взаимопроникновения сравнительной геномики и системной биологии, обсуждаемые в данной главе, приводят нас к следующему ключевому обобщению.
Многие, чтобы не сказать все, общие закономерности геномной и молекулярно-фенотипической эволюций описываются стохастическими процессами, основанными на принципе подверженной ошибкам репликации и ограниченными очищающим отбором, который поддерживает существующую общую (но не специфическую) архитектуру генома и устройства клеток.
Это обобщение не следует понимать как исключение адаптации из числа важнейших эволюционных понятий. Разумеется, адаптация – это общее и неотъемлемое явление в эволюции всех форм жизни. Тем не менее становится все более ясным, что общие количественные характеристики геномной архитектуры, функционирования и эволюции в первую очередь определяются неадаптивными, стохастическими процессами. Адаптация только модулирует эти закономерности. Здесь становится очень соблазнительным провести вполне очевидную параллель с нейтральной теорией Кимуры. В ходе высокоуровневого анализа геномных и молекулярно-фенотипических параметров мы начинаем различать контуры "неонейтрализма" (см. также гл. 8).
Аналогия между эволюцией и стохастическими физическими процессами ни в коем случае не отрицает метафоры "эволюции как мастерового" Жакоба. Напротив, новые открытия в эволюционной геномике прекрасно вписываются в это представление об эволюции: естественный отбор (адаптивный компонент эволюции) представляет собой процесс "латания", не полную перестройку или создание нового объекта, а добавление к существующему новых частей из уже имеющихся подручных материалов. Таким образом, первичная форма отбора – это очищающий отбор, который поддерживает статус-кво. Это обобщение имеет довольно удивительное, но неизбежное следствие: большая часть наиболее значимых событий во всей истории жизни произошла в течение первых нескольких сотен миллионов лет существования жизни на Земле, до появления современного типа клеток. Этот период в истории жизни должен был качественно отличаться от всей остальной эволюции; есть основания считать, что важнейшее достижение эволюции – это появление клетки, все остальное уже не так важно. Мы будем обсуждать происхождение жизни с этой точки зрения в главах 11 и 12 и вернемся к обсуждению общей природы эволюции в главе 13.
Параллели между эволюционной биологией и статистической физикой оказались точными и фундаментальными до такой степени, что кажется вполне справедливым заключение о том, что это не аналогии, а проявление общих статистических принципов (если не сказать законов) поведения больших ансамблей слабовзаимодействующих объектов. Как в физике, так и в эволюционной биологии такие ансамбли (например, идеальный газ в физике и геном как сумма генов в биологии) являются идеализациями. В реальности отклонения от поведения, которое предсказывается простыми статистическими моделями, неизбежны и значимы. В эволюционной биологии такие отклонения, кроме всего прочего, вызываются различными взаимодействиями генов, что приводит к неожиданным эффектам, таким как отсутствие строгой корреляции между биологической значимостью гена и скоростью его эволюции. Тем не менее существенный эвристический потенциал прямого статистического подхода в объяснении по крайней мере некоторых фундаментальных свойств как физических, так и биологических процессов неоспорим.
Рекомендуемая дополнительная литература
Barabasi, A. L., and Z. N. Oltvai. (2004) Network Biology: Understanding the Cell’s Functional Organization. // Nature Reviews Genetics 5: 101–113.
Обзор свойств биологических сетей с акцентом на масштабной инвариантности.
Barton, N. H., and J. B. Coe. (2009) On the Application of Statistical Physics to Evolutionary Biology. Journal of Theoretical Biology 259: 317–324.
Технически сложная, но важная работа по термодинамическому подходу в эволюционной биологии.
Drummond, D. A., and C. O. Wilke. (2009) The Evolutionary Consequences of Erroneous Protein Synthesis. Nature Reviews Genetics 10: 715–724.
Критический обзор концепции эволюции, ограниченной ошибками трансляции и ошибками укладки белка.
Lobkovsky, A. E., Y. I. Wolf, and E. V. Koonin. (2010) Universal Distribution of Protein Evolution Rates As a Consequence of Protein Folding Physics. Proceedings of the National Academy of Sciences USA 107: 2,983-2,988.
В этой работе эволюционная динамика выводится в рамках простой модели укладки белка и с хорошей точностью воспроизводится универсальное распределение эволюционных скоростей.
Koonin, E. V., and Y. I. Wolf. (2006) Evolutionary Systems Biology: Links Between Gene Evolution and Function // Current Opinion in Biotechnology 17: 481–487.
Обзор корреляций между эволюционными и молекулярно-фенотипическими параметрами.
Koonin, E. V., Y. I. Wolf, and G. P. Karev. (2002) The Structure of the Protein Universe and Genome Evolution // Nature 420: 218–223.
Обсуждение универсальных распределений и зависимостей с акцентом на роли стохастических процессов и принципе предпочтительного присоединения.
Molina, N., and E. van Nimwegen. (2009) Scaling Laws in Functional Genome Content Across Prokaryotic Clades and Lifestyles // Trends in Genetics 25: 243–247.
Последние данные по универсальным степенным функциям для различных функциональных классов генов.
Sella, G., and A. E. Hirsh. (2005) The Application of Statistical Physics to Evolutionary Biology // Proceedings of the National Academy of Sciences USA 102: 9,541-9,546.
Богатая идеями статья, детально описывающая формальную аналогию между статистической физикой и эволюционной динамикой.
Schroedinger, Erwin. (1944/1992) What Is Life?: With "Mind and Matter" and "Autobiographical Sketches". Cambridge, MA: Cambridge University Press. [Шредингер Э. Что такое жизнь? Физический аспект живой клетки / Пер. с англ. 3-е изд. Ижевск: РХД, 2002.
Небольшая классическая книга, которую можно порекомендовать еще раз как взгляд на биологию с физической точки зрения, не так уж и изменившийся со времен Шредингера.