• ничто из вышеперечисленного.
85. Два противоположных суждения о двух разных предметах:
• должны быть одновременно истинными;
• должны быть одновременно ложными;
• должны быть: одно – истинным, другое – ложным;
• могут быть какими угодно по истинности.
86. Два противоречащих суждения о двух разных предметах не могут быть:
• одновременно истинными;
• одновременно ложными;
• одно – истинным, другое – ложным;
• ни истинным и ни ложным каждое.
87.
Мы гуляли по Неглинной,
Заходили на бульвар,
Нам купили синий-синий,
Презеленый, красный шар.С. В. Михалков
В этом шуточном четверостишии преднамеренно нарушен логический закон:
1) тождества;
2) противоречия;
3) достаточного основания;
4) силлогизма;
5) парадокса;
6) стихотворения.
88. Закон противоречия нарушен в следующем высказывании:
• "Я знаю только то, что я ничего не знаю" (Сократ).
• "В детстве у меня не было детства" (А. П. Чехов).
• "История учит только тому, что она никого ничему не учит" (Г. Гегель).
• "Самое непостижимое в мире заключается в том, что он постижим" (А. Эйнштейн).
• "Слышу умолкнувший звук божественной эллинской речи" (А. С. Пушкин – по поводу перевода "Иллиады" Гомера, сделанного Н. И. Гнедичем).
• Во всех вышеприведённых высказываниях.
• Ни в одном из вышеприведённых высказываний.
89. В рассуждении: "Мёд не любит, чтобы его переливали, доливали, перемешивали и сильно нагревали, так как от этого он теряет свои лечебные свойства, как и от добавления воды и сахара. Между тем иногда такой мёд поступает в продажу. Образуется он в результате скармливания сахарного сиропа пчёлам", – нарушен закон:
• двойного отрицания;
• исключённого третьего;
• противоречия;
• тождества;
• достаточного основания.
90. В 1907 г. кадетская фракция в Государственной думе по вопросу об отношении к правительству решила: не выражать ему ни доверия, ни недоверия, причём если будет внесена резолюция доверия правительству, то голосовать против неё, а если будет внесена резолюция недоверия правительству, то голосовать против неё.
В этом решении нарушен логический закон:
• исключённого третьего;
• достаточного основания;
• неверного утверждения;
• подмены основания;
• двойного противопоставления;
• взаимозаменяемости.
91. В самый солнцепёк, вернувшись домой, Насреддин попросил жену: "Принеси-ка мне миску простокваши, нет ничего полезней и приятней для желудка в такую жару!" Жена ответила: "Да у нас – не то, что миски – даже ложки простокваши нет в доме!" Насреддин сказал: "Ну и хорошо, что нет, простокваша ведь вредна человеку".
В словах Насреддина нарушен логический закон:
• нестрогой дизъюнкции;
• противоречия;
• достаточного основания;
• двойного отрицания;
• основного заблуждения;
• порочного круга.
92. В данном рассуждении: "Немецкий физик Вальтер Нернст, автор третьего начала термодинамики (о недостижимости абсолютного нуля температуры) доказывал, что ему удалось завершить разработку фундаментальных законов термодинамики. Так: у первого начала было три автора (Ю. Майер, Д. Джоуль, Г. Гельмгольц), у второго – два (Н. Карно, Р. Клаузиус), у третьего – один (В. Нернст); следовательно, число авторов четвёртого начала должно равняться нулю, т. е. такого закона просто не может быть", – нарушен логический закон:
• подмены тезиса;
• порочного круга;
• двойного противоречия;
• исключённого тождества;
• достаточного основания;
• недостаточной истинности.
93. Импликация ложна только тогда, когда:
• её основание и следствие истинны;
• её основание и следствие ложны;
• её основание ложно, а следствие истинно;
• её основание истинно, а следствие ложно.
94. Символическая логика является разделом:
• формальной логики;
• философии;
• математики;
• грамматики.
95. Противоречия бывают:
• контактными и дистантными;
• явными и неявными;
• реальными и мнимыми;
• какими угодно из перечисленных;
• никакими из перечисленных.
96. Принцип верификации – это:
• распространённый софистический приём;
• критерий научного знания;
• основание индуктивных ошибок;
• одно из правил силлогизма;
• важный метод псевдонауки;
• главное требование аналогии.
97. В рассуждении: "Все птицы имеют крылья, следовательно, все существа с крыльями – это птицы", – нарушен логический закон:
• исключённого третьего;
• индуктивного силлогизма;
• сокращённого софизма;
• дедуктивной аналогии;
• ни один из перечисленных.
98. Энтимема – это:
• разновидность научной индукции;
• неразрешимое противоречие;
• вид сложного суждения;
• сокращённый простой силлогизм;
• аналогия с достоверными выводами.
99. Рассуждение: "Докажем, что три раза по два будет не шесть, а четыре. Возьмём спичку или палочку и сломаем её пополам. Это один раз два. Потом возьмём одну из половинок и её тоже сломаем пополам. Это второй раз два. Затем возьмём оставшуюся половинку и её тоже сломаем пополам. Это третий раз два. Итак, три раза по два будет четыре, а не шесть", – является:
• парадоксом;
• апорией;
• антиномией;
• силлогизмом;
• софизмом;
• бессмыслицей;
• философемой.
100. Сорит – это разновидность:
• логического парадокса;
• трудноразрешимого софизма;
• неполной индукции;
• сложного суждения;
• нулевого понятия;
• простого силлогизма.
Ответы
1. наука о формах и законах мышления
2. в античности
3. аристотелевской
4. Аристотель
5. построено по форме: "Все A – это B"
6. в ХIХ в.
7. стихийно сформированное в процессе жизненного опыта знание форм и принципов правильного мышления
8. софисты
9. форма мышления
10. объём
11. слова или словосочетания
12. наиболее важные признаки того объекта, который оно выражает13. объектов, охватываемых этим понятием
14. единичное
15. абстрактное
16. положительное
17. ни одна из перечисленных
18. все перечисленные
19. неясным по содержанию и нерезким по объёму
20. родовым
21. соподчинения
22. круговыми схемами Эйлера
23. рис. 42
24. известный футболист, футболист, негр, китаец
25. A = B = C
26. растение, дерево, сосна.
27. B C A D
28. круговым
29. непонятным для большей части людей
30. объём
31. подмена основания
32. художественные романы бывают детективными, фантастическими, историческими, любовными и другими
33. изделие человека
34. сломанный карандаш
35. единичное понятие
36. высокий уровень преступности
37. форма мышления
38. повествовательного предложения
39. суждение
40. субъектом
41. E
42. несовместимости
43. экзистенциальным
44. Человек – это разумное живое существо
45. Некоторые учёные являются древними греками
46. ни субъект, ни предикат не распределены
47. Все квадраты – это геометрические фигуры
48. речь идёт о части объектов, входящих в объём этого термина
49. все не птицы не являются воробьями
50. подчинения
51. неопределённым по истинности
52. импликацией
53. конъюнкцией
54. истинным
55. истинны все её элементы
56. истинен только один её элемент, а остальные – ложны
57. (((a → b) ∧ (c → d)) ∧ (¬ b ∨ ¬ d)) → (¬ a ∨ ¬ c)
58. форма мышления
59. силлогизмами
60. вид умозаключения
61. фигуру
62. средний термин
63. взаимное расположение его терминов и набор простых суждений, входящих в него
64. расширение большего термина
65. учетверение терминов
66. разновидность умозаключения
67. дизъюнктивное и категорическое
68. неполное деление
69. нестрогая дизъюнкция
70. утверждение от следствия к основанию
71. чисто условным
72. эквивалентно-категорическим
73. условно-разделительным
74. простой деструктивной дилеммой
75. из нескольких частных случаев выводится одно общее правило76. ни одна из вышеназванных
77. после этого, значит по причине того
78. неизвестна причинная связь явлений
79. конъюнкцией
80. вид умозаключения
81. все её элементы ложны
82. закон тождества
83. ученики нарушили закон тождества
84. ничто из вышеперечисленного
85. могут быть какими угодно по истинности
86. ни истинным и ни ложным каждое
87. противоречия
88. ни в одном из вышеперечисленных высказываний
89. закон тождества
90. исключённого третьего
91. противоречия
92. достаточного основания
93. её основание истинно, а следствие ложно
94. разделом математики
95. какими угодно из перечисленных
96. критерий научного знания
97. ни один из перечисленных
98. сокращённый простой силлогизм
99. софизмом
100. простого силлогизма
100 занимательных задач
Предлагаемые в этой книге задачи значительно различаются как по типу своего построения, так и по уровню сложности. Одни из них близки к математике, и для их решения надо будет составить простое уравнение, другие не имеют с ними ничего общего. Некоторые задачи предполагают знание нескольких простых законов физики, некоторые являются логическими упражнениями и головоломками, а некоторые представляют собой просто шутки, розыгрыши или фокусы. Одни задачи очень просты – вы сможете их решить за считанные секунды, а над другими, наоборот, надо изрядно поломать голову. В некоторых случаях не обойтись без карандаша и бумаги – в других придётся составить схему или нарисовать рисунок. Может потребоваться калькулятор или какие-нибудь предметы домашнего обихода. Однако при всех различиях между этими задачами они сходны между собой в том, что для их решения требуется нестандартный подход и работа воображения, – поэтому они и называются занимательными. Решение этих задач способствует развитию внимания, памяти, гибкости ума, которую также часто называют смекалкой, или находчивостью.
Ко всем задачам приводятся ответы и комментарии, однако не спешите в них заглядывать, попытайтесь самостоятельно найти верное решение. Чем больше этих задач вы сможете решить, тем проще и легче будете в дальнейшем справляться с задачами подобного типа и даже научитесь самостоятельно их составлять.
Сборник задач поможет вам интересно и с пользой провести часы досуга, скоротать время в длительном путешествии, найти тему разговора или разрядить затянувшуюся неловкую паузу в беседе с малознакомыми людьми, а также он пригодиться в различных иных жизненных ситуациях.
Условия задач
1. В каждом из 10 мешков находится по 10 монет. Каждая монета весит 10 г. Но в одном мешке все монеты фальшивые – не по 10 г., а по 11 г. Как с помощью только одноразового взвешивания определить, в каком мешке находятся фальшивые монеты (все мешки пронумерованы от 1 до 10)? Мешки можно открывать и вытаскивать любое количество монет из каждого.
2. На всех трёх железных банках с печеньем перепутаны этикетки: "Овсяное печенье", "Песочное печенье" и "Шоколадное печенье". Банки закрыты, и вы можете взять только одно печенье из одной (любой) банки, а потом правильно расположить этикетки. Как это сделать?
3. В вашем шкафу лежит 22 синих носка и 35 чёрных носков.
Вам надо в полной темноте взять из шкафа пару носков. Сколько носков нужно взять, чтобы с гарантией получить совпадающую пару?
4. Старинным часам требуется 30 с, чтобы пробить 6 ч. За сколько секунд часы пробьют 12 ч?
5. В пруду растёт один лист лилии. Каждый день число листьев удваивается. На какой день пруд будет покрыт листьями лилии наполовину, если известно, что полностью он будет покрыт ими через 100 дней?
6. Пассажирский лифт поднимается на пятый этаж со скоростью вдвое большей, чем грузовой лифт, который идёт до третьего этажа.
Какой из этих двух лифтов придёт раньше: грузовой на третий этаж или пассажирский на пятый, если стартовали они с первого этажа одновременно?
7. Летит гусь. Навстречу ему – стая гусей. "Здравствуйте, 100 гусей," – говорит он им. Они отвечают: "Нас не 100 гусей; вот если бы нас было столько, сколько сейчас, да ещё столько, да ещё пол-столько и четверть-столько, да ещё ты, вот тогда нас было бы 100 гусей".
Сколько гусей летит в стае?
8. Докажем, что 3 = 7. Известно, что если над каждой частью равенства проделать одну и ту же операцию, то равенство останется неизменным. Отнимем у каждой части нашего равенства по пять: 3 – 5 = 7 – 5. Получится: – 2 = 2. Теперь возведём каждую часть равенства в квадрат: (– 2) = 2. Получится: 4 = 4, следовательно: 3 = 7. Найдите ошибку в этом рассуждении.
9. Как известно, в любом атоме есть ядро, размеры которого меньше размеров самого атома. Если размер атомного ядра равен 10 см, а размер всего атома равен 10 см, следовательно, ядро по размеру меньше самого атома в 2 раза: 12 : 6 = 2. Верно ли это утверждение?
Если нет, то во сколько раз атомное ядро меньше атома?
10. Можно ли на самолёте долететь до Луны? Надо принять во внимание, что самолёты снабжены реактивными двигателями, как и космические ракеты, и работают на том же топливе, что и они.
11. Можно ли иголкой проколоть пятидесятикопеечную монету?
12. Стандартный стакан (200 г) наполнен водой до краёв. Сколько булавок можно в него накидать, чтобы из стакана не вылилось ни капли воды?
13. У Иванова в кабинете висит портрет. Иванова спрашивают: "Кто изображён на этом портрете?" Иванов путано отвечает:
"Отец изображённого на портрете есть единственный сын отца говорящего". Кто изображён на портрете?
14. Миссионер попал в плен к дикарям, которые посадили его в темницу и сказали: "Отсюда только два выхода – один на свободу, другой к гибели; выбраться тебе помогут два воина – один говорит всегда правду, другой всегда лжёт, но неизвестно, кто из них лжец, а кто правдолюбец; ты можешь задать любому из них только один вопрос". Какой вопрос надо задать, чтобы выбраться на свободу?
15. В монастыре висят две верёвки из редкостного шёлка. Они прикреплены к середине потолка на расстоянии одного метра друг от друга и достигают пола. Вор-акробат хочет украсть как можно больше верёвки. Высота потолка 20 м. Вор знает, что если он спрыгнет или упадёт с высоты более 5 м, то не сможет выбраться из монастыря. Поскольку лестницы у него нет, ему остаётся только лезть по верёвке. Он нашёл способ украсть обе верёвки почти целиком. Как это сделать?
16. Девушка ехала в такси. По пути она так много болтала, что шофёр занервничал. Он сказал ей, что очень сожалеет, но не слышит ни слова, – поскольку его слуховой аппарат не работает, он глух как пробка. Девушка замолчала, но, когда они доехали до места, поняла, что водитель над ней подшутил. Как она догадалась?
17. Вы находитесь в каюте стоящего на якоре океанского лайнера. В полночь вода была на 4 м ниже иллюминатора и поднималась на 0,5 м/ч. Если эта скорость удваивается каждый час, то за какое время вода достигнет иллюминатора?
18. Три путешественника прилегли отдохнуть в тени деревьев и уснули. Пока они спали, шутники вымазали углём их лбы. Проснувшись и взглянув друг на друга, они начали смеяться, причём каждому из них казалось, что двое других смеются друг над другом.
Внезапно один из них перестал смеяться, так как сообразил, что его собственный лоб тоже испачкан. Как он об этом догадался?
19. Сдвинув только одну их четырёх спичек, сделайте квадрат (рис. 45). Спички нельзя ни гнуть, ни ломать:
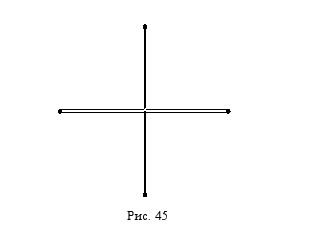
20. С восходом солнца путешественник начал подниматься по узкой, извилистой тропинке на вершину горы. Он шёл то быстрее, то медленнее, часто останавливаясь, чтобы отдохнуть. Проделав длинный путь, он достиг вершины только к закату солнца. Проведя ночь на вершине, с восходом солнца он отправился в обратный путь по той же тропинке. Спускался он также с неравномерной скоростью, неоднократно отдыхая по дороге, и к закату солнца достиг подножия горы. Понятно, что средняя скорость спуска превышала среднюю скорость подъёма. Есть ли на тропинке такая точка, которую путешественник проходил в одно и то же время суток как во время подъёма, так и во время спуска?
21. У скульптора есть 10 одинаковых статуй. Он хочет, чтобы у каждой из четырёх стен зала находилось по три статуи. Как их разместить?
22. Начертите, не отрывая карандаша от бумаги, следующие фигуры (рис. 46):
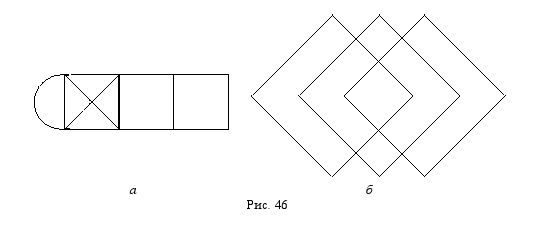
23. Один математик предложил торговцу такую сделку. Математик даёт торговцу 100 р., а торговец даёт математику взамен 1 к.
Каждый следующий день математик даёт торговцу на 100 р. больше, чем в предыдущий, т. е. на второй день он даёт ему 200 р., на третий – 300 р. и т. д. А торговец даёт математику взамен в два раза больше денег, чем в предыдущий день, т. е. на второй день он даёт ему 2 к., на третий – 4 к., на четвёртый – 8 к., на пятый – 16 к. и т. д.
Производить такой обмен они договорились в течение 30 дней. Кому из них этот обмен выгоден и почему?
24. Годовщина Октябрьской революции по старому стилю попадает на 25 октября, а по новому стилю – на 7 ноября. Таким образом, все события по старому стилю на 13 дней предшествуют тем же самым событиям по новому стилю. Значит, если по новому стилю Новый год приходится на 1 января, то по старому стилю он должен попадать на 19 декабря. Почему же мы тогда отмечаем старый Новый год 14 января?
25. Из спичек сделан рисунок рюмки, наполненной вином (рис. 47). Переставьте две спички так, чтобы на вновь получившем рисунке вино оказалось вне рюмки. При демонстрации роль вина может сыграть спичка: