9) П - Р - bd - K;
10) ЗУ - Р - df - Ж;
11) площадка f - остановка.
В данном случае площадка f оказалась достижимой (недостижимыми являются площадки i, k, l , m). Выделив коридоры, которые остались желтыми (ab, bc, cd, df), получим путь от a к f (abcdf, указанный на рис. 257 жирными дугами).
4. Общие свойства алгоритмов. Богатый опыт разработки и применения алгоритмов подсказывает ряд общих свойств, которые детализируют приведенное выше описание.
Дискретность алгоритма. Любой алгоритм можно рассматривать как процесс последовательного построения величин, идущий в дискретном времени по определенному предписанию, называемому программой. В начальный момент задается конечная совокупность величин (исходные данные), а в каждый следующий момент совокупность величин получается по программе из совокупности, имевшейся в предыдущий момент.
Детерминированность алгоритма. Совокупность величин, получаемых в какой-то (не начальный) момент времени, однозначно определяется совокупностью величин, полученных в предшествующие моменты времени. Например, алгоритм поиска пути в лабиринте допускает произвол в выборе коридора при наличии нескольких зеленых коридоров, отходящих от данной площадки. Чтобы сделать его строго детерминированным, необходимо добавить предписание о выборе зеленого коридора ( например, первый по часовой стрелке).
Направленность алгоритма. Если способ получения последующей величины из какой-нибудь заданной не приводит к результату, то должно быть указание, что´ надо считать результатом алгоритма. Иначе говоря, алгоритм через конечное число тактов времени (шагов) должен привести к остановке, которая свидетельствует о достижении требуемого результата. Так, при поиске пути в лабиринте остановка наступает либо на достижимой площадке, либо при возвращении на исходную площадку, если указанная цель недостижима.
- 623 -
Массовость алгоритма. Алгоритм служит для решения целого класса задач, причем начальная совокупность величин может выбираться из некоторого множества. Например, в алгоритме Евклида числа a и b выбираются из бесконечного (счетного) множества целых числе, а в алгоритме поиска пути в лабиринте начальная и конечная площадки выбираются из конечного множества площадок лабиринта. В математике проблема считается решенной, если для нее найден общий алгоритм.
Элементарность шагов алгоритма. Предписание о получении последующей совокупности величин из предшествующей должно быть простым и локальным. Это означает, что соответствующая операция должна быть элементарной для исполнителя алгоритма (человека ли машины). Например, встречающиеся в алгоритме Евклида операции сравнения, вычитания и перестановки чисел можно было бы расчленить на более простые операции, если бы они не считались достаточно стандартными и привычными. В то же время сам алгоритм Евклида может фигурировать в качестве элементарной операции более сложного алгоритма.
5. Ассоциативное исчисление. Дальнейшее обобщение понятия алгоритма связано с ассоциативным исчислением, которое строится на множестве всех слов в данном алфавите.
Напомним, что алфавит представляет собой любую конечную систему различных символов, называемых буквами. Любая конечная последовательность n букв некоторого алфавита является словом длины n в этом алфавите. Например, в алфавите из трех букв {a, b, c} словами будут последовательности b, ac, bac, abba, cbcccacabca и т.д. Пустое слово, не содержащее ни одной буквы, обычно обозначается через ∧. если слово L является частью слова M, то говорят о вхождении слова L в слово M. Например, в слове abcbcbab имеются два вхождения слова bcb и одно вхождение слова ba.
В качестве операций ассоциативного исчисления определяется система допустимых подстановок, с помощью которых одни слова преобразуются в другие. Подстановка вида L-M, где L и M - слова в том же алфавите, означает замену вхождения левой части правой, равно как и замену правой части левой. Иначе говоря, если в некотором слове R имеется одно или несколько вхождений слова L, то каждое из этих вхождений может заменяться словом M, и наоборот, если имеется вхождение слова М, то его можно заменить словом L. Например, подстановка ab-bcb применима четырьмя способами к слову abcbcbab. Замена каждого из двух вхождений bcb даст слова aabcbab и abcabab, а замена каждого из двух вхождений ab дает слова bcbcbcbsb, abcbcbbcb. В то же время к слову bacb эта подстановка не применима. Подстановка вида Р-∧ означает, что из преобразуемого слова выбрасывается вхождение слова Р,
- 624 -
а также что между двумя какими-либо буквами преобразуемого слова или впереди него, или за ним вставляется слово Р.
Итак, ассоциативное исчисление - это множество всех слов в некотором алфавите вместе с какой-нибудь конечной системой допустимых подстановок. Очевидно, чтобы задать ассоциативное исчисление, достаточно определить алфавит и систему допустимых подстановок (например, алфавит {a, b, c, d, e} и система подстановок ac-ca, ad-da, bc-cb, bd-db, abac-abacc, eca-ae, edb-be).
6. Эквивалентность слов. Два слова называются эквивалентными, если одно из них можно получить из другого последовательным применением допустимых подстановок. Так, в приведенном выше (5) исчислении эквивалентными являются, например, слова abcde cadedb, что видно из следующих последовательных преобразований: abcde, acbde, cabde, cadbe, cadedb. Последовательность слов R1, R2, ..., Rn, когда каждое следующее слово является результатом однократного применения допустимой подстановки к предыдущему слову, образует дедуктивную цепочку, причем соседние слова в этой цепочке называют смежными. Очевидно, любые два слова в дедуктивной цепочке являются эквивалентными.
Эквивалентность слов L и M обозначается L ~ M и обладает всеми свойствами отношения эквивалентности (рефлексивность, симметричность и транзитивность). Если L ~ M, то при наличии в каком-либо слове R вхождения L в результате подстановки L-M получается слово, эквивалентное R. Например, воспользовавшись эквивалентностью abcde~cadbe, из слова bbabcdec получаем эквивалентное ему слово bbcadbec.
В каждом ассоциативном исчислении возникает своя специальная проблема слов, заключающаяся в следующем: для любых двух слов в данном исчислении требуется узнать, эквивалентны они или нет. Решение этой проблемы аналогично поиску пути в лабиринте, площадки которого соответствуют смежным словам. Очевидно, эквивалентность двух слов означает, что соответствующие им площадки связаны некоторым путем, который представляет собой дедуктивную цепочку от одного слова к другому. Однако проблема слов является далеко идущим обобщением задачи поиска пути в конечном лабиринта. Так как в любом ассоциативном исчислении содержится бесконечное множество различных слов, то соответствующий лабиринт имеет бесконечное число площадок, и, следовательно, решение вопроса об эквивалентности любых двух слов сводится к поиску пути в бесконечном лабиринте.
С помощью алгоритма перебора решается ограниченная проблема слов: требуется установить, можно ли одно из заданных слов преобразовать в другое применением допустимых подстановок не более, чем k раз, где k - произвольное, но фиксированное число. Для этого достаточно построить все слова, смежные с одним из заданных слов,
- 625 -
затем для каждого из полученных слов построить все слова, смежные с ним и т.д. всего k раз. В результате получим список всех слов, которые можно получить из заданного с помощью допустимых подстановок, применяемых не более k раз. Если второе заданное слово окажется в этом списке, то ответ на поставленный вопрос будет положительным, а если его в списке нет, ответ отрицательный. Можно заметить, что ограниченная проблема слов соответствует ограничению лабиринта таким образом, что расстояние между рассматриваемыми площадками не превышает k коридоров.
Однако такой путь принципиально не пригоден для решения неограниченной проблемы слов. Поскольку длина дедуктивной цепочки, простирающейся между эквивалентными словами (если такая цепочка существует), может оказаться сколь угодно большой, то не существует никакой возможности указать такое конечное число k, которое гарантирует решение проблемы путем простого перебора. Поэтому для получения желаемых результатов необходимо применять другие идеи, основанные на анализе самого механизма преобразования слов посредством допустимых подстановок.
В некоторых случаях могут быть обнаружены и использованы свойства, остающиеся неизменными для всех слов дедуктивной цепочки (дедуктивные инварианты). Так, в каждой из допустимых подстановок исчисления из (5) левая и правая части содержат одно и то же число вхождений буквы а. Следовательно, в любой дедуктивной цепочке все слова также должны содержать одно и то же число вхождений буквы а. На основе этого дедуктивного инварианта можно установить, какие слова не могут быть эквивалентными (например, слова abacdac и abaadac - не эквивалентны).
Проблема слов в ассоциативном исчислении имеет огромное значение в связи с тем, что к ней сводятся многие геометрические, алгебраические и логические задачи. Так, любую формулу логики высказываний и предикатов можно трактовать как слова в некотором алфавите, содержащем логические символы, высказывания, предикаты и предметные переменные. Процесс эквивалентного преобразования или вывода логического следствия может быть представлен как преобразование слов, причем роль допустимых подстановок играют логические законы или аксиомы. Таким образом, вопрос о выводимости какой-либо формулы становится вопросом существования дедуктивных цепочек, ведущих от слов, представляющих посылки, к словам, представляющим следствие. В ряде интерпретаций ассоциативного исчисления, в частности в теории вывода, используются ориентированные подстановки вида L → M, которые допускают лишь подстановку слева направо (слова L в слово M). Это соответствует лабиринтам, по каждому коридору которого можно двигаться только в одном направлении.
- 626 -
7. Нормальный алгоритм Маркова. Система допустимых подстановок в некотором алфавите, снабженная точным предписанием о порядке и способе их использования, позволяет осуществить детерминированный процесс, который последовательно преобразует некоторое слово в новые слова, эквивалентные исходному. Говорят, что задан алгоритм в алфавите А, который применим к слову L и перерабатывает его в слово М, если, отправляясь от L и действуя согласно предписанию, в конце концов получают М, на котором процесс обрывается. Множество слов, к которым применим данный алгоритм, называют его областью применимости. Два алгоритма в некотором алфавите называются эквивалентными, если области их применимости совпадают и результаты переработки или любого слова из общей области применимости также совпадают.
Важный шаг на пути уточнения понятия алгоритма сделан А.А. Марковым, который дал стандартные раз и навсегда определенные указания о порядке использования подстановок. Определение нормального алгоритма Маркова сводится к следующему.
Задается алфавит А и фиксируется в определенном порядке система ориентированных подстановок. Исходя из произвольного слова R в алфавите А, просматриваются подстановки в том порядке, в каком они заданы. Первая встретившаяся подстановка с левой частью входящей в R, используется для преобразования R, в которое вместо первого вхождения ее левой части подставляется ее правая часть, в результате чего получаем новое слово R1. Далее процесс повторяется, исходя из слова R1, R2 и т.д. до тех пор, пока этот процесс не останавливается. Признаками остановки процесса служат два случая: во-первых, когда получается такое слово Rn, что ни одна из левых частей допустимых подстановок в него не входят, и во-вторых, когда при получении Rn приходится применять последнюю подстановку.
Пусть, например, задан алфавит A = {1, +} и система подстановок + → ∧, 1→ 1 (∧ - пустое слово). Слово 111+11+1111+1 этот алгоритм перерабатывает так:
111+11+1111+1
11111+1111+1
111111111+1
1111111111
1111111111
Процесс оканчивается применением заключительной подстановки, которая перерабатывает слово само в себя. Как видим, алгоритм суммирует количество единиц, т.е. осуществляет операцию сложения. Эквивалентный ему алгоритм можно задать с помощью системы подстановок: 1+ → +1; +1→1; 1→1.
- 627 -
В соответствии со смелой гипотезой, основанной на накопленном опыте, предполагается, что любой алгоритм может быть представлен в виде нормального алгоритма Маркова. Иначе говоря, нормальный алгоритм Маркова принимается в качестве стандартной формы любого алгоритма.
8. Машина Тьюринга. Другой стандартной формой представления любого алгоритма являются функциональные схемы, реализуемые в машинах Тьюринга (рис. 258). Слова, перерабатываемые в данном алфавите {ξ1, ξ2, ..., ξm}, называемом внешним алфавитом машины, изображаются в ячейках неограниченной ленты (НЛ), причем в каждой в ячейке может храниться только один символ.
Работа машины происходит в дискретном времени. На каждом такте обозревается единственная ячейка и считываемый символ ξi заменяется другим ξj (i = j означает, что символ не изменяется), который определяется состоянием машины sk в данный тактовый момент из множества ее возможных состояний {s1, s2, ..., sn}. Кроме того, вырабатывается последующее состояние машины и команда, управляющая перемещением по ленте, которая подготавливает очередную ячейку для обозрения на следующем такте. Таких команд в машине Тьюринга только три: П - обозревать соседнюю справа ячейку, Л - обозревать соседнюю слева ячейку и Н - продолжать обозревать прежнюю ячейку. Совокупность {s1, s2, ..., sn} и {П, Л, Н} образует внутренний алфавит машины.
Функциональная схема, соответствующая какому-либо алгоритму, задается подобно общей таблице переходов конечного автомата (6.4) с некоторыми несущественными отличиями. Обычно строки таблицы соответствуют символам внешнего алфавита ξ1, ξ2, ..., ξm, а столбца - состояниям машины s1, s2, ..., sn. В каждой клетке записывается тройка символов, обозначающих замещающих символ из внешнего алфавита, управляющую команду и последующее состояние. Например, функциональная схема, соответствующая алгоритму сложение (числа представляются совокупностью единиц или просто "палочек", общее количество которых равно данному числу, причем они расположены в ячейках без пропусков) имеет вид:
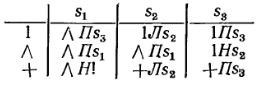
Знак "!" используется для обозначения стоп-состояния, при наступлении которого процесс останавливается и результирующее слово считывается по ленте, а через ∧ обозначается пустой символ.
Функциональная таблица полностью определяет функционирование машины и реализуется в ней логическим блоком (ЛБ). На
- 628 -
два его входа подаются считываемые символы, над которыми совершаются операции (замена другими символами), и состояния, играющие роль команд, определяющих эти операции. На одном из выходов логического блока образуется символ, который в данном такте замещает на ленте обозреваемый символ, а на остальных двух выходах - команды, определяющие функционирование машины на следующем такте (перемещение по ленте и новое состояние). Для запоминания этих команд вводятся задержки З1 и З2 представляющие собой внутреннюю память машины.
Перед началом работы на ленту наносится исходное слово и задаются начальные условия, т.е. указывается первая обозреваемая ячейка и начальное состояние. После пуска машины процесс преобразования информации происходит автоматически.