Трудность связывания внешней реальности с консенсусной взяла новый рекорд высоты с открытием квантовой механики. Это выразилось в продолжающихся по сей день спорах между физиками о том, как интерпретировать эту теорию, хотя прошло уже почти 100 лет. Внешняя реальность описывается гильбертовым пространством (гл. 8), в котором волновая функция меняется со временем детерминистическим образом, тогда как в консенсусной реальности события кажутся случайными, с распределением вероятности, которое можно с высокой точностью вычислить по волновой функции. Прошло более 30 лет после рождения квантовой механики, прежде чем Эверетт показал, как эти две реальности могут быть согласованы, и ещё 10 лет мир ждал открытия декогеренции, ключевого явления для примирения существования макросуперпозиций во внешней реальности с их отсутствием в консенсусной.
Сейчас главным вызовом для теоретической физики является объединение квантовой механики с гравитацией. Основываясь на приведённой последовательности исторических примеров, я предсказываю, что корректная математическая теория квантовой гравитации побьёт все прежние рекорды по сложности её интерпретации. Допустим, накануне следующей конференции по квантовой гравитации наш джинн залетит в лекционный зал и запишет на доске уравнения окончательной теории. Сможет ли кто-либо из участников понять то, что будет стёрто следующим утром? Я сомневаюсь.
Итак, направление наших поисков понимания реальности разделяется на два, которыми можно заниматься по отдельности: великим вызовом для когнитивистики является понимание связи консенсусной реальности с нашей внутренней реальностью, а великим вызовом для физики является понимание связи нашей консенсусной реальности с внешней реальностью. Обе задачи обескураживают своей трудностью. В консенсусной реальности камень кажется непроницаемым, твёрдым и неподвижным объектом, однако за исключением квадриллионной части своего объёма камень является пустым пространством между частицами, испытывающими постоянные вибрации. Наша консенсусная реальность кажется трёхмерной сценой, на которой во времени разворачиваются события, но эйнштейновская работа (гл. 11) говорит о том, что изменение - это иллюзия, время - не более чем четвёртое измерение неизменного пространства-времени (которое никогда не создавалось, никогда не уничтожается и содержит всю космическую историю, как DVD содержит фильм). Квантовый мир кажется случайным, но работа Эверетта говорит о том, что случайность также является иллюзией, просто способом, каким наше сознание отмечает, когда оно клонируется в расходящихся параллельных вселенных. Мир квантовой гравитации ощущается… - ну, здесь физикам остаётся ещё мно-о-ого работы.
Далее мы сконцентрируемся на поисках в области физики и доведём их до логического предела: на что, с учётом известного о консенсусной реальности, может быть похожа внешняя реальность? Какова её истинная природа?
Резюме
• Хотя существует лишь одна истинная реальность, есть несколько дополнительных точек зрения на неё.
• Во внутренней реальности нашего сознания единственная информация, которую мы имеем о внешней реальности - это небольшая выборка, доставляемая органами чувств.
• Эта информация подвергается сильным искажениям и, судя по всему, говорит о работе органов чувств и мозга ничуть не меньше, чем о внешней реальности.
• Математическое описание внешней реальности, открытое теоретической физикой, сильно отличается от того, как мы воспринимаем внешнюю реальность.
• На пути между внутренней и внешней реальностями лежит "консенсусная реальность" - общее описание физического мира, с которым согласны все самосознающие наблюдатели.
• "Главный вопрос жизни, Вселенной и всего такого" распадается на две части, исследуемые по отдельности. Задачей физических наук является вывод консенсусной реальности из внешней, а задачей когнитивистики - вывод внутренней реальности из консенсусной.
• Оставшаяся часть книги посвящена первой из этих двух задач.
Глава 10. Физическая и математическая реальности
Философия написана в той величественной Книге (я имею в виду Вселенную), которая всегда открыта нашему взору, но читать её может лишь тот, кто сначала освоит язык и научится понимать знаки, которыми она начертана. Написана же она на языке математики, и знаки её - треугольники, окружности и другие геометрические фигуры, без которых нельзя понять ни единого из стоящих в ней слов и остаётся лишь блуждать в тёмном лабиринте.
Галилео Галилей
"Пробирных дел мастер" (1623)
Невероятная эффективность математики в естественных науках есть нечто граничащее с мистикой, ибо никакого рационального объяснения этому факту нет.
Юджин Вигнер
(1960)
Заканчивая пятничным утром в Принстоне разбирать электронные сообщения по поводу сочинения книги, ремонта микроволновки и полемики вокруг квантового суицида, я неожиданно нашёл в почтовом ящике настоящую жемчужину - письмо от одного из именитых профессоров, своего знакомого.
Дата: 4 декабря 1998, 07:17:42 EST
Тема: Письмо, которое было непросто написать
Уважаемый Макс!
…Ваши безумные статьи не идут вам на пользу. Прежде всего, подавая их в хорошие журналы и имея несчастье добиться их публикации, вы губите их "забавную" сторону… Я редактор ведущего журнала… и ваша статья никогда бы у меня не прошла. Это, пожалуй, не так уж важно, за исключением того, что коллеги считают эти ваши личные особенности дурным знаком в плане перспектив… Вы должны понять, что если полностью не отделите эту деятельность от своих серьёзных исследований, возможно, вовсе её прекратив, и не перенесёте её в паб или другое подобное место, то можете поставить под угрозу своё будущее.
Меня словно окатили ледяной водой, но это был один из тех замечательных моментов, когда я понял, что поставил новый личный рекорд, и у меня появилась новая высота, которую надо попробовать взять. Когда я переслал письмо отцу, он ответил цитатой из Данте: segui il tuo corso et lascia dir le genti, то есть: "Следуй своей дорогой, и пусть люди говорят, что угодно".
Меня всегда забавляет, насколько сильно у физиков стадное чувство, притом что все мы на словах привержены нешаблонному мышлению и готовы отвергать авторитеты. Я заметил это ещё студентом: например, революционная эйнштейновская теория относительности не заслужила Нобелевской премии, сам Эйнштейн отвергал фридмановское открытие расширения Вселенной, а Хью Эверетт не смог получить постоянную работу в области физики. Иначе говоря, отвергались куда более важные открытия, чем те, которые я, реалистично глядя на вещи, могу надеяться совершить. Так что ещё в студенчестве я столкнулся с дилеммой: я полюбил физику именно за то, что был очарован её величайшими вопросами, но, похоже, что если я буду просто следовать зову сердца, то следующим местом моей работы станет "Макдоналдс".
Я не хотел выбирать между любовью и карьерой, так что разработал секретную стратегию, которая действует на удивление хорошо, позволяя мне заодно зарабатывать на пропитание. Я называю её "стратегией доктора Джекила и мистера Хайда". Джордано Бруно в 1600 году заживо сожгли за нетрадиционные взгляды (в числе которых убеждённость в бесконечности космоса), а Галилея приговорили к пожизненному домашнему аресту за то, что он доказывал обращение Земли вокруг Солнца. Современные санкции стали мягче. Если вы интересуетесь масштабными, философского характера вопросами, большинство физиков будет относиться к вам так же, как если бы вы увлекались компьютерными играми: чем заниматься после работы - ваше личное дело и ваше хобби не будут ставить вам в упрёк, если оно не отвлекает от дел и если вы не говорите о нём слишком много на работе. Так что, когда авторитетные фигуры спрашивают, чем я занимаюсь, я превращаюсь в респектабельного доктора Джекила и говорю, что работаю над мейнстримными вопросами космологии (вроде разобранных в гл. 4), включая многочисленные измерения, цифры и т. д. Но когда никто не смотрит, я превращаюсь в злого мистера Хайда и делаю то, что действительно хочу делать: ищу истинную природу реальности (гл. 6, 8 и большинство оставшихся глав этой книги). Чтобы не вызывать беспокойства, я написал у себя на сайте, что у меня есть "побочные интересы", и пошутил, что на каждые десять мейнстримных статей позволяю себе написать одну вздорную. Это было очень удобно, поскольку подсчётами никто, кроме меня, не занимался. Ко времени своей защиты в Беркли я напечатал восемь статей, но половину их написал мистер Хайд, так что в диссертации я их не упоминал. Мне очень нравился мой научный руководитель в Беркли Джо Силк, но я следил, чтобы он оказывался подальше от принтера, когда я печатал статьи мистера Хайда. Я показал их ему лишь после того, как он подписал мою диссертацию… Я продолжаю придерживаться этой стратегии: всякий раз, когда я ищу работу или обращаюсь за исследовательским грантом, я упоминаю лишь о работе доктора Джекила, а параллельно продолжаю исследовать "большие вопросы", которые поддерживают во мне огонь - в хорошем, а не в бруновском смысле.
Эта стратегия превзошла самые смелые мои ожидания, и я весьма благодарен судьбе за возможность работать в университете с замечательными коллегами и студентами, не переставая думать о том, что меня сильнее всего интересует. Но теперь я считаю, что я в долгу перед научным сообществом и пришло время платить по обязательствам. Если представить, что все исследовательские темы выстроены перед вами в шеренгу в метафорическом пространстве, то есть некая граница, отделяющая то, что является мейнстримной физикой, от того, что в неё не входит. У этой границы удивительное свойство: она постоянно смещается (рис. 10.1)! На некоторых участках она сжимается, оставляя теории от алхимии до астрологии за пределами мейнстрима. В других - расширяется, и идеи вроде теории относительности или микробной природы заболеваний переходят из области спекуляций меньшинства в общепризнанную науку. Я давно уверен, что есть области, в которых физики могут сделать ценный вклад, несмотря на то, что эти темы сначала кажутся чересчур философскими. Мой нынешний контракт достаточно продолжителен, чтобы у меня не было оснований от них отстраняться: я считаю, что сейчас мой моральный долг перед более молодыми учёными вывести мистера Хайда из академического чулана и внести свой вклад в изменение этих границ. Вот почему мы с Энтони Агирре основали Институт фундаментальных вопросов, о котором я упоминал в гл. 8 (http://fqxi.org). И поэтому я пишу эту книгу.
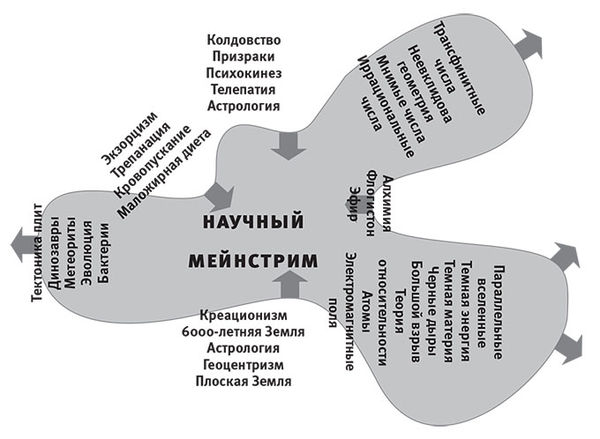
Рис. 10.1. Граница того, что считается мейнстримом, постоянно меняется.
Так какая же из моих статей вызвала столь острую реакцию: остановитесь - или сломаете карьеру? Чему столь далёкому от нынешней границы мейнстрима (рис. 10.1) была она посвящена, что этот профессор почувствовал необходимость вернуть меня в лоно науки? Она была о том, что наш физический мир - это гигантский математический объект. И в этой главе мы начнём его изучать.
Математика, везде математика
Каков же ответ на главный вопрос жизни, Вселенной и всего такого? В книге "Автостопом по Галактике" Дугласа Адамса выясняется, что ответ на этот вопрос - 42, однако самой сложной частью задачи оказалось отыскание самого вопроса. В действительности, хотя наши любознательные предки задавались глобальными вопросами, их поиски "теории всего" менялись вместе с ростом знаний. По мере того как древние греки заменяли мифологические объяснения механическими моделями Солнечной системы, их акценты в этих вопросах смещались с почему на как.
С тех пор сфера наших вопросов сократилась в одних областях и разрослась в других (рис. 10.1). Некоторые вопросы отброшены как наивные или ошибочные, вроде объяснения размеров планетных орбит исходя из первичных принципов (это было популярно в эпоху Возрождения). То же самое может случиться с модными нынче попытками предсказания количества тёмной энергии в космосе, если окажется, что её плотность в наших окрестностях является исторической случайностью (гл. 6). Тем не менее наша способность отвечать на другие вопросы превзошла самые смелые ожидания прежних поколений. Ньютон был бы поражён, узнав, что мы сумели определить возраст Вселенной с точностью до 1 % и узнали устройство микромира в достаточной мере, чтобы сконструировать "Айфон".
Я считаю шутку Дугласа Адамса про 42 очень удачной, поскольку математика играет исключительную роль во всех этих успехах. Та идея, что Вселенная в некотором смысле является математической, восходит по меньшей мере к пифагорейцам и породила многовековую дискуссию физиков и философов. Галилей утверждал, что Вселенная - это "величественная книга", написанная на языке математики. Лауреат Нобелевской премии по физике Юджин Вигнер в 60-х годах XX века настаивал, что "невероятная эффективность математики в естественных науках" нуждается в объяснении.
Фигуры, паттерны и уравнения
Мы переходим к рассмотрению по-настоящему радикального объяснения. Однако прежде необходимо уточнить, что именно мы пытаемся объяснить. Пожалуйста, оторвитесь на несколько секунд от чтения и оглядитесь. Где вся эта математика, которой мы собираемся заниматься? Разве математика - это не наука о числах? Вероятно, вам на глаза попадётся несколько чисел, например пагинация в этой книге, но это лишь символы, изобретённые и изображённые людьми, так что вряд ли они отражают математическую сущность Вселенной в каком-либо глубоком смысле.
Из-за нашей системы образования многие приравнивают математику к арифметике. Но математика, как и физика, пришла к постановке более глубоких вопросов. Например, в приведённой выше цитате Галилей говорит о геометрических фигурах вроде окружностей и треугольников как о математических. Видите ли вы вокруг себя геометрические узоры или фигуры? (Дизайн вроде прямоугольной формы книги не в счёт.) Но попробуйте бросить камешек и посмотрите, какую красивую форму придаёт природа его траектории! Галилей сделал замечательное открытие (рис. 10.2): траектория любых предметов имеет одинаковую форму, называемую перевёрнутой параболой. Более того, форму этой параболы можно описать простым уравнением: x = y, где x - горизонтальное положение, y - вертикальное положение (высота). В зависимости от начальной скорости и направления эта форма может растягиваться и по вертикали, и по горизонтали, однако она всегда остаётся параболой.