1. Скорость света в пустом пространстве всегда постоянна независимо от движения источника или приемника света.
2. В двух системах координат, движущихся прямолинейно и равномерно друг относительно друга, все законы природы строго одинаковы, и нет никакого средства обнаружить абсолютное прямолинейное и равномерное движение.
Существует много экспериментов, подтверждающих оба этих положения, и нет ни одного, который бы противоречил какому-либо из них. Первое положение выражает постоянство скорости света, второе обобщает принцип относительности Галилея, сформулированный для механических явлений, на все явления, происходящие в природе.
В механике мы видели, что если скорость материальной точки относительно одной системы координат такая-то, то она будет иной в другой системе, движущейся прямолинейно и равномерно относительно первой. Это вытекает из простых принципов механического преобразования. Они непосредственно даны нашей интуицией (человек, движущийся относительно корабля и берега), и, очевидно, здесь нет никакой ошибки! Но этот закон преобразования находится в противоречии с постоянством скорости света. Другими словами, мы прибавляем третий принцип.
3. Координаты и скорости преобразуются от одной инерциальной системы к другой согласно классическому преобразованию.
Противоречие очевидно. Мы не можем объединить три указанных выше принципа.
Классическое преобразование кажется слишком очевидным и простым, чтобы попытаться изменить его. Мы уже пытались изменить первые два принципа и пришли к несогласию с экспериментом. Все теории движения эфира требовали изменения первых двух принципов. Но это не приносило никакой пользы. Еще раз мы убеждаемся в серьезности наших трудностей. Необходим новый путь. Это путь признания первого и второго положения исходными и, хотя это и кажется странным, отказа от третьего положения. Новый путь начинается с анализа наиболее фундаментальных и простых понятий. Мы покажем, как этот анализ вынуждает нас изменить наши старые взгляды и устраняет все наши трудности.
Время, пространство, относительность
Наши новые предположения суть:
1. Скорость света в вакууме одинакова во всех системах координат, движущихся прямолинейно и равномерно друг относительно друга.
2. Все законы природы одинаковы во всех системах координат, движущихся прямолинейно и равномерно друг относительно друга.
Теория относительности начинается с этих двух положений. С этого времени мы не будем применять классическое преобразование, так как знаем, что оно противоречит исходным положениям.
В данном случае, как и всегда в науке, важно отказаться от глубоко укоренившихся, часто некритически повторяемых предрассудков. Так как мы видели, что изменения обоих положений приводят к противоречию с экспериментом, то должны иметь смелость твердо установить их справедливость и напасть на один, возможно слабый, пункт, а именно: на способ, которым координаты и скорости преобразуются от одной системы координат к другой. Мы хотим сделать выводы из этих двух положений, посмотреть, где и как эти положения противоречат классическому преобразованию, и найти физический смысл полученных результатов.
Можно еще раз использовать пример с движущейся комнатой и наблюдателями внутри и вне ее. Пусть световой сигнал опять излучается из центра комнаты, и вновь мы спрашиваем обоих людей, что они обнаружат, допустив только два вышеуказанных принципа и забыв то, что было предварительно сказано о среде, сквозь которую проходит свет. Приведем их ответ.
Внутренний наблюдатель: Световой сигнал, идущий от центра комнаты, достигнет стен одновременно, так как все стены одинаково отстоят от источника света, а скорость света одинакова во всех направлениях.
Внешний наблюдатель: В моей системе координат скорость света совершенно такая же, как и в системе наблюдателя, движущегося вместе с комнатой. Мне нет дела до того, движется ли источник света в моей системе или нет, так как его движение не влияет на скорость света. То, что я вижу, это световой сигнал, идущий с постоянной скоростью, одинаковой во всех направлениях. Одна из стен стремится убежать от светового сигнала, а другая - приблизиться к нему. Поэтому убегающая стена будет достигнута световым сигналом немного позднее, чем приближающаяся. Хотя эта разность времен прибытия светового сигнала будет очень незначительной, если скорость комнаты мала по сравнению со скоростью света, тем не менее световой сигнал не достигнет обеих противоположных стен, расположенных перпендикулярно к направлению движения, совершенно одновременно.
Сравнивая предсказания обоих наблюдателей, мы обнаруживаем крайне удивительный результат, который явно противоречит несомненно хорошо обоснованным понятиям классической физики. Оба события - достижение стен двумя световыми лучами - одновременны для наблюдателя внутри и не одновременны для наблюдателя вне комнаты. В классической физике у нас были одни часы, одно течение времени для всех наблюдателей во всех системах. Время, а стало быть, и такие слова, как "одновременно", "ранее", "позднее", имели абсолютное значение, не зависящее от какой-либо системы. Два события, происходящих в одно и то же время в одной системе координат, происходили одновременно во всех системах координат.
Предположения 1 и 2, т. е. теория относительности, вынуждают нас отказаться от этого взгляда. Мы описали два события, которые происходят одновременно в одной системе координат, но в разное время в другой системе. Наша задача - понять это следствие, понять смысл предложения: "два события, одновременные в одной системе координат, могут быть не одновременны в другой системе".
Что мы обозначаем словами "два одновременных события в одной системе координат"? Интуитивно каждый человек считает, что он понимает смысл этого выражения. Но будем осторожными и постараемся дать строгие определения, так как мы знаем, как опасно переоценивать интуицию. Ответим сначала на простой вопрос.
Что такое часы?
Примитивное субъективное чувство течения времени позволяет нам упорядочить наши впечатления, судить о том, что одно событие происходит раньше, другое позднее. Но чтобы показать, что промежуток времени между двумя событиями равен десяти секундам, нужны часы. Благодаря применению часов понятие времени становится объективным. В качестве часов может быть использовано любое физическое явление, если только оно может быть повторено столько раз, сколько необходимо. Если мы возьмем интервал между началом и концом такого события за единицу времени, то любые интервалы времени можем измерить повторением этого физического процесса. Все часы, от простых песочных до наиболее совершенных, основаны на этой идее. При пользовании песочными часами единицей времени будет являться интервал, в течение которого песок высыпается из верхней емкости в нижнюю. Тот же физический процесс может быть повторен перевертыванием часов.
Пусть в двух отдаленных друг от друга точках пространства находится двое идеально идущих часов, точно показывающих одинаковое время. Это положение будет справедливым, несмотря на ту осторожность, с которой мы его проверяем. Но что это означает в действительности? Как можем мы удостовериться, что удаленные друг от друга часы всегда показывают одинаковое время? Можно использовать один из возможных методов - телевидение. Легко понять, что телевидение берется как пример; само по себе оно несущественно для наших доводов. Я мог бы стоять около одних часов и смотреть на изображение других часов на экране телевизора. Тогда я мог бы судить, показывают ли часы одновременно одинаковое время или нет. Но это не было бы хорошим доказательством. Изображение в телевизоре передается электромагнитными волнами, следовательно, распространяется со скоростью света. На экране телевизора я вижу изображение, посланное некоторое очень короткое время тому назад, в то время как на часах, стоящих возле меня, я вижу то, что происходит в настоящий момент. Эту трудность можно легко преодолеть. Для этого нужно рассмотреть изображения обоих часов в точке, одинаково отстоящей от каждых из них, т. е. рассмотреть их в точке, лежащей на середине расстояния между часами. Тогда, если сигналы посланы одновременно, они достигнут меня в один и тот же момент. Если двое хороших часов, наблюдаемых в точке, находящейся посредине между ними, показывают одинаковое время, то они вполне подходят для указания времени событий в двух отдаленных точках.
В механике мы употребляли только одни часы. Но это было не очень удобно, потому что мы должны были производить все измерения вблизи этих часов. Смотря на удаленные от нас часы, например с помощью телевизора, мы всегда должны помнить следующее: то, что мы видим теперь, в действительности произошло раньше; так, мы видим свет от Солнца спустя восемь минут после того, как свет излучен. Во все показания часов мы должны вносить поправки, соответствующие нашему расстоянию от часов.
Поэтому неудобно иметь только одни часы. Однако теперь, поскольку мы знаем, как проверить, показывают ли двое или вообще несколько часов одновременно одно и то же время, и идя тем же самым путем, мы легко можем вообразить себе в данной системе координат столько часов, сколько нам хочется.
Каждые из них помогут нам определить время событий, происходящих в непосредственном соседстве с ними. Все часы находятся в покое относительно системы координат. Они являются "хорошими" часами; они синхронизированы, это означает, что часы одновременно показывают одинаковое время.
В нашей расстановке часов нет ничего удивительного или странного. Вместо одних-единственных часов мы применяем теперь много синхронизированных часов и поэтому можем легко проверить, одновременны ли два отдаленных события в данной системе координат или нет. Они одновременны, если синхронизированные часы вблизи них показывают одинаковое время в момент, когда происходят события. Теперь утверждение, что одно отдаленное событие происходит раньше другого, имеет определенный смысл. Его можно проверить с помощью синхронизированных часов, покоящихся в нашей системе координат.
Все это находится в согласии с классической физикой и не вызывает еще противоречий с классическим преобразованием.
Для определения одновременности событий часы синхронизируются с помощью сигналов. В наших рассуждениях существенно то, что сигналы передаются со скоростью света, со скоростью, которая играет такую фундаментальную роль в теории относительности.
Так как мы хотим заняться важной проблемой о двух системах координат, движущихся прямолинейно и равномерно относительно друг друга, то мы должны рассмотреть два стержня, снабженных часами. В каждой из обеих систем, движущихся друг относительно друга, наблюдатель имеет теперь свой собственный масштаб со своим собственным набором часов, жестко связанным с масштабом.
При измерениях в классической механике мы употребляли одни часы во всех системах координат. Теперь мы имеем много часов в каждой системе координат. Это различие несущественно. Одни часы были достаточны, но никто не может возражать против употребления многих часов, пока они ведут себя как хорошо синхронизированные часы.
Теперь мы приближаемся к существенному пункту, показывающему, где классическое преобразование противоречит теории относительности. Что происходит, когда двое часов движутся прямолинейно и равномерно друг относительно друга? Физик, придерживающийся классических взглядов, ответил бы: "Ничего. Их ритм остается одинаковым, и мы можем употреблять для показания времени движущиеся часы, так же как и покоящиеся". Таким образом, согласно классической физике, два события, одновременные в одной системе координат, будут одновременными в любой другой системе.
Но это не единственный возможный ответ. Мы можем столь же легко представить себе движущиеся часы, имеющие ритм, отличный от ритма покоящихся часов. Обсудим теперь эту возможность, не решая пока вопроса о том, изменяют ли на самом деле часы свой ритм при движении или нет. Что означает утверждение, что движущиеся часы изменяют свой ритм? Предположим ради простоты, что в верхней системе координат у нас только одни часы, а в нижней - много. У всех часов одинаковый механизм и нижние часы синхронизированы, т. е. они показывают одновременно одинаковое время. Мы изобразили (рис. 63) три последовательных положения обеих систем, движущихся друг относительно друга. На первом рисунке положения стрелок верхних и нижних часов ради удобства взяты одинаковыми; так мы их поставили сами. Все часы показывают одинаковое время. На втором рисунке мы видим относительные положения обеих систем спустя некоторое время. Все часы в нижней системе показывают одинаковое время, но часы в верхней системе вышли из общего ритма. Их ритм изменился, и время отличается вследствие того, что часы движутся относительно нижней системы. На третьем рисунке мы видим, что различие в положении стрелок со временем увеличилось. Наблюдатель, покоящийся в нижней системе координат, нашел бы, что движущиеся часы изменили свой ритм. Конечно, тот же результат получился бы, если бы часы двигались по отношению к наблюдателю, покоящемуся в верхней системе координат; в этом случае в верхней системе должно было бы быть много часов, а в нижней - только одни. Закон природы должен быть одинаков в обеих системах, движущихся друг относительно друга.
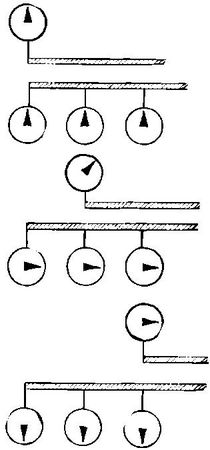
Рис. 63
В классической механике молчаливо предполагалось, что движущиеся часы не изменяют своего ритма. Это казалось столь очевидным, что едва ли было достойно упоминания. Но ничто не должно считаться вполне очевидным; если мы действительно желаем быть осторожными, мы должны подвергать анализу все положения, принимаемые в физике.
Нельзя считать какое-либо положение бессмысленным только потому, что оно отличается от положения классической физики. Мы можем легко представить себе, что движущиеся часы изменяют свой ритм, если закон этого изменения одинаков для всех инерциальных систем отсчета.
Еще один пример. Возьмем метровый стержень; это значит, что длина стержня - один метр, пока он находится в покоящейся системе координат. Пусть он движется прямолинейно и равномерно, скользя вдоль масштаба, представляющего систему координат. Будет ли его длина и в этом случае равна одному метру? Мы должны знать заранее, как определять его длину. Пока стержень был в покое, его концы совпадали с нанесенными на масштабе отметками, расстояние между которыми равнялось одному метру. Из этого мы заключили: длина покоящегося стержня равна одному метру. Как мы измеряем длину этого стержня во время движения? Это можно было бы сделать следующим образом. В данный момент два наблюдателя делают одновременно моментальные фотоснимки начала движущегося стержня и его конца. Поскольку снимки сделаны одновременно, мы можем сравнить, с какими отметками масштаба совпадают начало и конец движущегося стержня. Таким путем мы определим его длину. Нужно, чтобы два наблюдателя отметили одновременные события, происходящие в различных частях данной системы. Нет никаких оснований считать, что результат таких измерений будет таким же, как и в случае, когда отрезок покоится. Поскольку фотографии должны быть сделаны одновременно, а одновременность, как мы знаем, является относительным понятием, зависящим от системы координат, то кажется вполне возможным, что результаты этих измерений будут различными в различных системах, движущихся друг относительно друга.
Мы легко можем представить, что не только движущиеся часы изменяют свой ритм, но и движущийся стержень изменяет свою длину, если законы изменений одинаковы для всех инерциальных систем.
Мы лишь обсуждали некоторые новые возможности, не приводя каких-либо оправданий в пользу их принятия.
Мы помним: скорость света одинакова во всех инерциальных системах отсчета. Этот факт несовместим с классическим преобразованием. Круг должен быть где-то разорван. Нельзя ли это сделать как раз здесь? Не можем ли мы предположить, что ритм движущихся часов и длина движущегося стержня изменяются как раз так, что постоянство скорости света будет следовать непосредственно из этого предположения? В самом деле, можно! Здесь впервые теория относительности и классическая физика радикально расходятся. Наш вывод может быть сформулирован иначе: если скорость света одинакова во всех системах, то движущиеся стержни должны изменять свою длину, движущиеся часы должны изменять свой ритм, а законы, управляющие этими изменениями, должны быть так же точно определены.
Во всем этом нет ничего таинственного или неразумного. В классической физике всегда предполагалось, что часы и в движении, и в покое имеют одинаковый ритм, что масштабы и в движении, и в покое имеют одинаковую длину. Если скорость света одинакова во всех системах координат, если теория относительности справедлива, то мы должны пожертвовать этим положением. Трудно освободиться от глубоко укоренившихся предрассудков, но другого пути нет. С точки зрения теории относительности старые понятия кажутся произвольными. Почему надо верить, как это мы делали раньше, в абсолютное время, текущее одинаково для всех наблюдателей во всех системах? Почему надо верить в неизменяемое расстояние? Время определяется часами, пространственные координаты - масштабами, и результат этих определений может зависеть от поведения этих часов и масштабов, когда они находятся в движении. Нет оснований считать, что они будут вести себя так, как нам этого хотелось бы. Косвенное наблюдение, а именно наблюдение электромагнитных явлений, показывает, что движущиеся часы изменяют свой ритм, а масштаб - длину, в то время как, основываясь на механических явлениях, мы и не думали, что такое может быть. Мы должны принять понятие относительного времени в каждой системе координат, ибо это наилучший выход из трудностей. Дальнейший научный успех, достигнутый теорией относительности, показывает, что новый взгляд не должен рассматриваться как печальная необходимость, ибо успехи теории относительности оказались весьма значительными.
До сих пор мы старались показать, что´ привело к основным положениям теории относительности и как теория относительности вынуждала нас пересматривать и изменять классическое преобразование, по-новому трактуя понятия времени и пространства. Наша цель - указать идеи, образующие основу новых физических и философских взглядов. Эти идеи просты; но в той форме, в какой они здесь сформулированы, они недостаточны для того, чтобы получить выводы не только качественные, но и количественные. Мы опять должны применить наш старый метод объяснения только принципиальных идей и формулировки некоторых выводов без доказательства.
Чтобы сделать ясным различие между взглядом старого физика (назовем его С), верящего в классическое преобразование, и взглядом нового физика (назовем его Н), признающего теорию относительности, вообразим следующий диалог между ними.
С: Я верю в принцип относительности Галилея в механике, ибо я знаю, что законы механики одинаковы в двух системах, движущихся прямолинейно и равномерно друг относительно друга или, другими словами, что эти законы инвариантны относительно классического преобразования.