Часть II. Неметаллы
Глава 4
Торможение трещины, или как обеспечить вязкость
Плиний старший (23-79 гг. н.э.) в своей весьма путаной "Естественнойистории" указывает способ, с помощью которого можно отличить неподдельныйалмаз. Он советует положить предполагаемый алмаз на наковальню и ударитьего тяжелым молотом как можно сильнее. Если камень не выдержит, он не настоящийалмаз. Надо думать, так было уничтожено немало драгоценных камней - ведьПлиний путает здесь твердость и вязкость. Алмаз - самый твердый из всехвеществ, и его твердость очень полезна в тех случаях, когда необходиморезать, царапать или шлифовать; в этом состоит его главное применение втехнике. Но алмаз, как и другие твердые драгоценные камни, довольно хрупок;и если бы даже его добывали большими кусками и в больших количествах, широкораспространенным конструкционным материалом он бы не был.
Самый тяжкий грех конструкционного материала - не недостаток прочностиили жесткости, которые, конечно, совершенно необходимы, а недостаток вязкости,иными словами - недостаточное сопротивление распространению трещин. Можнопримириться с недостатком прочности или жесткости и учесть их в процессеконструирования, но бороться с трещинами, которые оказываются очень опасными,застигая инженера врасплох, намного труднее.
Большинство металлов и пород дерева, резина, стеклопластики, кости,зубы, одежда, канаты, нефрит - вязки. Большинство минералов, стекла, посуднаякерамика, канифоль, бакелит, бетон, печенье - хрупки. Хрупким можно назватьи обычное желе, это легко проверить за столом, наблюдая, как распространяютсяв нем трещины от ложки или вилки. Вещества, которые мы перечислили в каждомиз списков, имеют довольно мало общего, вот почему не так просто выявитьто, что делает одни вещи вязкими, а другие - хрупкими. В то же время различиемежду хрупкостью и вязкостью очень осязаемо. Обожженная глина и кусок жестиимеют примерно одинаковую прочность на разрыв. Но если вы уроните на полглиняный горшок, он разлетится вдребезги, а с упавшей консервной банкойничего не случится - в худшем случае на ней появится небольшая вмятина.Прочность на разрыв обычных стекол и керамик может быть довольно большой,но никому не придет в голову делать из них, например, автомобиль. Причинаясна - очень уж они хрупки. Здравый смысл подсказывает это каждому из нас.Но почему? Что же такое хрупкость на самом деле?
Прежде всего, скорость нагружения - далеко не главное, что определяетхрупкость. Психологически существует большая разница между статическойнагрузкой, которая прикладывается медленно, и динамической мгновенно приложеннойударной нагрузкой. Разница существует и на самом деле, и ею нельзя пренебречь,но она далеко не так важна, как это может показаться с первого взгляда.Мы стучим молотком не потому, что нам нужны удары сами по себе, а потому,что удар тяжелого молотка - очень удобный и дешевый путь получения большойлокальной силы. Если бы мы приложили такую же по величине силу медленно,то, как правило, получили бы примерно тот же конечный результат. Это справедливои в тех случаях, когда мы рассматриваем падение предметов на пол, автомобильныеаварии, крушения самолетов, хотя в дальнейшем в этих явлениях мы увидимнекоторые важные особенности. Однако независимо от того, медленно или быстроприкладывается сила к хрупкому телу, стоит только начаться разрушению -трещины будут распространяться в нем очень и очень быстро - обычно со скоростьюнесколько тысяч километров в час. Именно поэтому разрушение кажется наммгновенным.
Мы уже говорили, что в каком-то смысле нет существенной разницы междумеханически нагруженным материалом и взрывчаткой. Энергия деформации упругоготела накапливается в натянутых химических связях, а при разрушении телаэта энергия освобождается. Если достигнута теоретическая величина деформацииразрыва, все связи оказываются максимально натянутыми, и мы должны считать,что энергия деформации примерно равна энергии химических связей в материале.На практике, однако, материалы обычно разрушаются, не достигнув и малойтолики теоретической прочности, так что освобожденная энергия при этомнамного меньше, чем энергия, даваемая эквивалентным количеством взрывчатки.И все-таки разрушение может сопровождаться вполне ощутимым хлопком. Наблюдениеза тем, как разрываются особо прочные волокна или усы (например, в машинеМарша), убедительно показывает, что их прочность составляет значительнуюдолю теоретической. В этом случае после разрыва не найдешь, как обычно,кусков образца: после взрывообразного разрушения волокно исчезает, оставляялишь мелкую пыль. Такие испытания не опасны лишь потому, что прочные волокна,как правило, очень малы.
Ударная прочность
Здесь уместно прервать наш разговор об общей проблеме распространениятрещины и поговорить о некоторых особых эффектах, которые возникают придинамических, ударных нагрузках. Сначала напомним, что максимальная скорость,с которой может передаваться нагрузка через любое вещество, равна скоростизвука в этом веществе. В самом деле, звук можно представить себе как волнуили серию волн напряжений, проходящих через среду с характерной скоростью.
Скорость звука в веществе равна (E/ρ), где Е - модуль Юнга, a ρ- плотность данного вещества. Взяв обычные числовые значения величин Е и g для конструкционных материалов, мы увидим, что скорость звука в этих. материалахбудет очень большой. Для стали, алюминия и стекла она составит около18000-20000 км/час (~5000 м/сек), что значительно превышает скорость звука ввоздухе. Это также намного больше скорости удара молотка и значительно большескорости полета пули.
Время, в течение которого молоток или пуля действуют с какой-то силойна твердое тело, составляет около сотой доли секунды. А это очень долгоевремя: фотолюбители знают, как много всего может совершиться за одну сотую.Точно так же и в нашем случае сотая доля секунды намного больше времени,потребного для отвода энергии от точки удара. От этой точки при ударе излучаетсяцелая серия волн напряжений, которые распространяются по всему объему тела.Очень быстро, за время, скажем, около нескольких десятитысячных или стотысячныхдолей секунды, эти волны достигают противоположных границ тела и отражаютсяот них подобно эху, лишь очень немного уменьшаясь в интенсивности. Дальнейшийход событий определяется многими факторами, в том числе формой тела, местомудара и т.д. Очень может статься, что отраженные волны напряжений постояннобудут встречать в некоторой критической или "несчастливой" точке прямыеволны, идущие от места удара, и это нагромождение вызовет прогрессирующийрост напряжения в этой точке вплоть до разрушения. Рассказы о певцах, отголоса которых вылетали стекла в окнах, не так уж и фантастичны.
Можно привести интересные примеры поведения твердых тел под ударнойнагрузкой. Например, при исследовании керамик повседневно проводятся ударныеиспытания керамических пластинок - свободно опертая квадратная пластинкаподвергается удару заданной силы по центру верхней поверхности. Во многихслучаях пластинка разрушается не в точке удара. Часто случается, что отваливаютсячетыре угла пластинки, потому что волны напряжений сталкиваются именнов углах.
Иногда случается, что, попав в броню, снаряд не пробивает ее, но отвнутренней поверхности броневой плиты отлетает рваный кусок металла, осколок.Скорость и энергия этого осколка могут быть огромными, и разрушения, причиненныеим внутри, например, танковой башни, оказываются такими же, как если быснаряд действительно пробил броню.
Подобным же образом, когда снаряд или пуля попадает в бак с жидкостью,например в топливный бак самолета, выходное отверстие получается намногобольшим, и заделать его значительно труднее - ударные волны легко распространяютсячерез жидкость и вырывают кусок в задней части бака. Голова человека конструктивнонапоминает бак с жидкостью, и последствия попадания пули в нее, к сожалению,слишком хорошо известны. Менее известно, однако, что аналогичные событиямогут последовать за тупым ударом в лоб. При проектировании защитных касокзаботятся о том, как погасить ударную волну и предохранить затылок прилобовом ударе. Этой цели и служит внутренняя лента в каске, которая напервый взгляд кажется необходимой лишь для вентиляции.
В технике вязкость материала определяется обычно путем ударных испытанийобразца прямоугольного сечения размером 5-10 мм, часто снабженного стандартнымнадрезом. Образец закрепляют по концам, а затем разрушают тяжелым молоткомв форме маятника. Измеряя разницу между высотой, с которой маятник падална образец, и высотой, на которую он взлетел, разрушив его, определяютэнергию, затраченную на разрушение. Строго говоря, это испытание почтини о чем не говорит, но оно позволяет провести грубое сравнение различныхматериалов. Поэтому такие испытания очень популярны у инженеров.
Критерий Гриффитса и критическая длина трещины
Вернемся теперь к вопросу о распространении трещины в твердом теле.В данном случае для нас не имеет значения, статическая или динамическаянагрузка разрушает тело. Вообще говоря, если в данной точке достигнуторазрушающее напряжение, то разрушение произойдет независимо от того, какимпутем оно достигалось. Правда, существуют некоторые исключения: отдельныевещества, вроде вара или конфеты ириски, чувствительны к скорости нагружения.Даже дети знают, что самую неподатливую ириску легко разломить, ударивпо ней чем-нибудь. Иногда удар приводит к успеху там, где бесполезны медленныеприемы (глава 8). Обычно же материалы, как правило, меньше чувствуют разницумежду динамическим и статическим нагружением.
Конечно, идеально было бы иметь материал, в котором зарождение трещинсовершенно исключено. К сожалению, на практике такого, кажется, не бывает.Мы видели в предыдущей главе, что даже самая гладкая поверхность стеклаиспещрена мельчайшими невидимыми трещинами; более того, если бы удалосьполучить бездефектную поверхность, она вскоре стала бы дефектной из-засоприкосновений с другими телами. Следовательно, практически все определяетсялегкостью, с которой трещины распространяются в нагруженном материале.Основы теории распространения трещин были заложены все тем же Гриффитсом.
Гриффитс указал два условия, необходимых для распространения трещины.Во-первых, рост трещины должен быть энергетически выгодным процессом, и,во-вторых, должен работать молекулярный механизм, с помощью которого можетосуществиться преобразование энергии. Первое условие требует, чтобы налюбой стадии распространения трещины количество запасенной в теле энергииуменьшалось - подобно тому, как уменьшается потенциальная энергия автомобиля,спускающегося с горы. С другой стороны, и при энергетической выгоде автомобильможет спускаться с горы лишь в том случае, если у него есть колеса и ихне держат тормоза. Колеса в этом случае служат механизмом, с помощью которогоавтомобиль скатывается с горы, они обеспечивают преобразование энергии.
Как мы уже говорили, деформированное тело "начинено" энергией, котораяпредпочла бы высвободиться. Так, поднятый вверх камень имеет потенциальнуюэнергию и стремится упасть. Если материал полностью разрушен, энергия деформацииего, естественно, полностью освобождена. Рассмотрим, однако, что происходитна промежуточных этапах процесса разрушения. Когда в деформированном телепоявляется трещина, она слегка раскрывается и оба ее края расходятся нанекоторое расстояние. Это означает, что материал, непосредственно примыкающийк краям трещины, релаксирует, напряжения и упругие деформации в нем уменьшаются,и упругая энергия освобождается. Давайте проследим за трещиной, начавшейсяна поверхности тела и идущей в глубь нагруженного материала (рис. 29).Понятно, что область срелаксировавшего материала будет приблизительно соответствоватьдвум заштрихованным треугольникам. Общая площадь этих треугольников будетпримерно l (l - длинатрещины). Следовательно, количество освобожденной энергии должно быть пропорциональноквадрату длины трещины, или глубины ее проникновения в тело. Расчеты подтверждаютэту грубую оценку. Иными словами, трещина глубиной 2 микрона высвобождаетв 4 раза больше упругой энергии, чем трещина глубиной в микрон, и т.д.
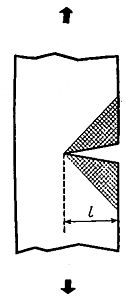
Рис. 29. Распространение трещины Гриффитса. С распространениемтрещины материал в заштрихованных областях разгружается, освобождая упругуюэнергию.
На другой чаше наших энергетических весов расположилась поверхностнаяэнергия 2Gl, которая необходима для образования двух новых поверхностей.Очевидно, эта энергия пропорциональна первой степени длины (или глубины)трещины. Величины поверхностной энергии двухмикронной и одномикронной трещинотличаются лишь в 2 раза, в то время как величины освобожденной энергиидеформации - в 4 раза. Последствия такого взвешивания достаточно ясны.Мелкая трещина для своего роста должна больше потреблять поверхностнойэнергии, чем производить свободной энергии вследствие релаксации напряжений.Эти условия невыгодны для роста трещины. Однако, если исходная трещинадостаточно велика, картина изменяется на противоположную: с ростом размероввеличина освобожденной энергии увеличивается быстрее, она ведь зависитот квадрата длины трещины. Получается, что, если длина трещины превышаетнекоторую "критическую длину Гриффитса", трещина производит больше энергии,чем потребляет. Тогда она может с громадной скоростью рвануться вперед,и процесс этот будет подобен взрыву. Для каждой величины напряжения в данномматериале существует своя критическая длина Гриффитса. Для теоретическимаксимальной величины напряжения (теоретической прочности) критическаядлина бесконечно мала, для материала, свободного от напряжений, она бесконечновелика - иного мы и не должны были ожидать. К сожалению, для тех напряжений,с которыми нам приходится обычно иметь дело, критическая длина трещины,как правило, очень мала, порядка нескольких микрон, и, конечно, она уменьшается,когда мы пытаемся увеличить напряжение. В этом заключается одна из трудностей,связанных с получением более прочных материалов.
Итак, при обычных уровнях нагружений все трещины, за исключением самыхмелких, имеют энергетический стимул к росту. Весь вопрос теперь в том,могут ли они расти. Иными словами, существует ли соответствующий механизмроста, то есть существует ли способ для реализации имеющейся энергетическойвыгоды, или преобразования одной формы энергии в другую? Гриффитсов балансэнергии, энергетическая выгода распространения трещины, длина которой превышаетнекоторую критическую величину, - явления совершенно общие для всех упругихтел. Но вот механизм преобразования энергии как раз и отличает вязкие материалыот хрупких.
Этим механизмом является концентрация напряжений. Как мы видели в главе3, концентрация напряжений на кончике трещины выражается приближенноформулой
K= 2(l/R),
где l - длина трещины, идущей с поверхности, или полудлина внутреннейэллиптической трещины, R - радиус ее кончика.
В типичном хрупком материале радиус кончика трещины R остаетсяпостоянным, он не зависит от длины трещины. Поэтому с ростом трещины концентрациянапряжений становится опаснее. На практике R имеет величину, сравнимуюс атомными размерами. Пусть R, скажем, 1 ангстрем. Тогда у кончикатрещины длиной около микрона (10000 А) напряжение, равное теоретическойпрочности, появится уже при очень умеренных средних по объему напряжениях.А такого размера трещина обычно соответствует гриффитсовой критическойдлине. Следовательно, трещина может расти, начиная примерно с этой длины,причем, конечно, момент начала роста сильно зависит от приложенной нагрузки.
Но после того, как трещина двинулась вперед, ситуация обостряется. Концентрациянапряжений увеличивается, баланс энергии все более и более склоняется впользу развития трещины. Если внешняя нагрузка не снимается, рост трещиныбыстро ускоряется и вскоре достигает максимально возможной величины (обычноона составляет приблизительно 38% от скорости звука). Для стекла это около6500 км/час (что и наблюдалось в эксперименте). Ну, а в это время волнынапряжений гуляют, наверное, в материале во всех направлениях со скоростьюзвука (то есть быстрее, чем распространяются трещины), отражаясь как отстарых, так и от вновь образовавшихся поверхностей, и дело закончится,вероятно, далеко не одной трещиной. Иными словами, материал разбиваетсявдребезги. Это оказывается возможным благодаря тому, что при больших напряженияхобщая упругая энергия материала "заплатит" за образование множества новыхповерхностей; в самом деле, при теоретической прочности она могла бы "рассчитаться"за разделение всего материала на слои толщиной в один атомный размер.
Совершенно хрупкие материалы вроде стекла достаточно надежны лишь приочень малых напряжениях. Стекло, например, можно использовать в витринемагазина, потому что в этом случае гриффитсова длина трещины достаточновелика и материал не боится небольших царапин или иных повреждений поверхности.Но если мы хотим работать с высокими уровнями напряжений, где-нибудь околотеоретической прочности стекла, мы не имеем права допускать появления наповерхности даже самых мельчайших трещин. Ведь стоит только одной трещинеувеличиться до критической длины (а она может быть порядка тысячи ангстрем- одной десятой микрона), как наступит катастрофическое разрушение. Именнопоэтому применение однородных хрупких материалов при серьезных нагрузкахчересчур опасно.
Нельзя сказать, что отсутствие у некоторых материалов способности сопротивлятьсяраспространению трещин казалось всегда недостатком первобытному человеку- он мог делать из кремня и обсидиана различные режущие инструменты. Практическиэти минералы представляют собой природные стекла. Если обладать необходимыминавыками, то легкого нажатия рукой на деревянный нож достаточно, чтобыотщепить длинную полоску минерала, которая сама может затем использоватьсяв качестве ножа. Обработка же нехрупких камней, таких, как нефрит, можетбыть выполнена только с помощью гораздо более трудоемкого процесса-шлифовки.Чаще всего растягивающие напряжения возникают в инструментах вследствиеизгиба, поэтому, придавая каменным инструментам компактные формы, можноне допустить больших напряжений и обеспечить достаточный срок их службы.Конечно, оружие типа каменного меча было бы совершенно непрактичным.