4) некоторые вкусные булочки привезены сегодня утром;
5) некоторые булочки с изюмом привезены сегодня утром;
6) все вкусные булочки мягкие;
7) все жесткие булочки невкусные;
8) сегодня утром не привозили булочек с джемом?
Задача Д32. Верно ли сделаны выводы? В чем разница
между задачами?
1) Гоголь написал "Мертвые души". На стене висит портрет Гоголя. Вывод: на стене висит портрет автора "Мертвых душ".
2) Какой-то человек изобрел самовар. На стене висит портрет какого-то человека. Вывод: на стене висит портрет изобретателя самовара.
Доказательство от противного
Задача ДЗЗ. Существует ли наименьшее положительное рациональное число?
Задача Д34. Каждый месяц Папа Карло зарабатывал разное число золотых и за год заработал всего 60 золотых. Докажите, что в какой-то из месяцев он заработал нецелое число золотых.
Задача Д35. По кругу написаны все целые числа от 1 до 2010 в таком порядке, что при движении по часовой стрелке числа поочередно то возрастают, то убывают. Докажите, что какие-то два четных числа стоят рядом.
Задача Д36! Можно ли бумажный круг разрезать на несколько частей по прямым линиям и дугам окружностей и составить из них квадрат той же площади?
Задача Д37Ї Каждый из голосующих на выборах вносит в избирательный бюллетень фамилии 10 кандидатов. На избирательном участке находится 11 урн. После выборов выяснилось, что в каждой урне лежит хотя бы один бюллетень и при всяком выборе 11 бюллетеней по одному из каждой урны найдется кандидат, фамилия которого встречается в каждом из выбранных бюллетеней. Докажите, что по крайней мере в одной урне все бюллетени содержат фамилию одного и того же кандидата.
Равносильность
Задача Д38. Каково наибольшее число утверждений из приводимых ниже, которые одновременно могут быть истинными?
1) Джо ловкач.
2) Джо не везет.
3) Джо везет, но он не ловкач.
4) Если Джо ловкач, то ему не везет.
5) Джо является ловкачом тогда и только тогда, когда ему везет.
6) Либо Джо ловкач, либо ему везет, но не то и другое одновременно.
Метаголоволомки
Задача Д39. Илье Муромцу, Добрыне Никитичу и Алеше Поповичу за верную службу дали 6 монет: 3 золотых и 3 серебряных. Каждому досталось по две монеты. Илья Муромец не знает, какие монеты достались Добрыне, а какие Алеше, но знает, какие монеты достались ему самому. Придумайте вопрос, на который Илья Муромец ответит "да", "нет" или "не знаю" и по ответу на который вы сможете понять, какие монеты ему достались.
Задача Д40. Мудрец встретил трех человек. Он знал, что среди них есть рыцарь, хитрец и лжец. Мудрец спросил первого: "Вы кто?" Тот ответил. "По такому ответу я не могу узнать, кто он", – подумал мудрец. Тогда он спросил о том, кем является первый, остальных двух. Они ответили, и все три ответа оказались разными по смыслу. Тогда мудрец подумал и сказал: "Теперь понятно". Кто же был этот первый?
Задача Д41. Судье известно, что из двух подозреваемых А и Б один – рыцарь, а другой – шпион, который может как лгать, так и говорить правду. Судья спросил у А, шпион ли Б. После ответа А он сразу понял, кто шпион. Кто же?
Задача Д42*. Перед судом предстали трое обвиняемых: А, Б и В. Суду было известно, что один из них рыцарь, другой лжец, а третий шпион (способный как говорить правду, так и лгать). Но кто есть кто, суд не знал.
Подсудимого А судья спросил:
– Вы шпион?
А ответил односложно ("да" или "нет"). Тогда судья спросил обвиняемого Б:
– Сказал ли А правду?
Ответил Б также односложно ("да" или "нет"). В этот момент А заявил:
– Обвиняемый В не шпион.
Судья ответил:
– Я и раньше знал это, а теперь я знаю, кто шпион.
1) Кто шпион?
2) Что сказал Б?
Задача Д43*. В некотором королевстве живут граждане трех типов: а) дурак считает всех дураками, а себя умным; б) скромный умный про всех знает правильно, а себя считает дураком; в) уверенный умный про всех знает правильно, а себя считает умным. В думе 200 депутатов. Премьер-министр провел анонимный опрос думцев: сколько умных в этом зале сейчас находится? По результатам опроса он не смог понять ответ. Но тут из поездки вернулся единственный депутат, не участвовавший в опросе. Он ответил на вопрос про всю думу, включая себя, и, увидев этот ответ, премьер-министр всё понял. Сколько умных в думе могло быть (включая путешественника)?
Задача Д44*. Из колоды вынули 7 карт, показали всем, перетасовали и раздали Грише и Леше по 3 карты, а оставшуюся карту
1) спрятали;
2) отдали Коле.
Гриша и Леша могут по очереди сообщать вслух любую информацию о своих картах. Могут ли они сообщить друг другу свои карты так, чтобы при этом Коля не смог вычислить местонахождение ни одной из тех карт, которых он не видит? (Гриша и Леша не договаривались о каком-либо особом способе общения; все переговоры происходят открытым текстом.)
Задача Д45*. Петя, Дима, Миша, Саша и Илья играют в мафию. Среди них два мафиози, два мирных жителя и комиссар. Мафиози знают только друг друга, комиссар знает роль каждого, мирные жители не знают роли других игроков. Мафиози всегда лгут. Комиссар и мирные жители говорят правду. Мальчики сделали следующие заявления (в указанном порядке):
Петя: "Я не знаю, кто Дима".
Дима: "Я знаю, кто комиссар".
Миша: "Я знаю, кто Петя".
Саша: "Я знаю, что Миша – комиссар".
Кто Илья?
Задача Д46*. Трое гусаров ехали по улице друг за другом. Каждому в руки упало по цветку от девушек на балконе. Гусары знают, кто был в строю, но каждый видел только, кто и в каком порядке ехал впереди него и кто им бросал цветы (а кто бросил ему самому – не знает). Полковник видел только то, что его дочь бросила цветок ровно одному из этих гусаров, и гусары тоже это знают. Полковник знает, кто именно ехал, но в каком порядке – не знает. Он может вызывать гусаров поодиночке и задавать им вопросы, на которые те честно отвечают "Так точно", "Никак нет" или "Не могу знать". Как полковнику за три вопроса узнать, кому из них бросила цветок его дочь?
Задача Д47*. Хватит ли полковнику из предыдущей задачи четырех вопросов, чтобы узнать, кому из четырех гусаров бросила цветок его дочь? А десяти вопросов, если гусаров было десять?
Мудрецы и колпаки
Во всех задачах этого и следующего разделов считается, что мудрецы рассуждают быстро и безошибочно. Каждому известно, что остальные участники – тоже мудрецы. Если мудрец может точно ответить на заданный вопрос, он всегда честно отвечает. Если не может, то не пытается угадать, а говорит "Не знаю". Мудрецы, стоящие в колонне (в затылок друг другу), видят колпаки всех стоящих впереди, но не видят ни своего колпака, ни колпаков стоящих сзади мудрецов. Все мудрецы слышат ответы других мудрецов.
Задача Д48. Двум мудрецам принесли два черных и один белый колпак. Затем их поставили в затылок друг другу и надели на каждого по колпаку. После этого спросили сначала второго, а потом первого, знает ли он, какого цвета колпак на его голове. Второй мудрец сказал, что не знает. А первый правильно назвал цвет своего колпака. Какой именно?
Задача Д49. Трем мудрецам принесли три черных и два белых колпака. Затем их построили в затылок друг другу, после чего надели на каждого по черному колпаку. После этого стали по очереди спрашивать каждого мудреца, начиная с последнего, какого цвета у него колпак. На это мудрецы либо отвечают "Не знаю", либо называют цвет. Что будут отвечать мудрецы?
Задача Д50 Десяти мудрецам принесли по три желтых, синих, красных и зеленых колпака. Мудрецов построили в затылок друг другу и надели каждому по колпаку, а два оставшихся колпака спрятали. Затем по очереди, начиная с последнего, стали спрашивать каждого, какого цвета у него колпак. На это мудрецы либо отвечают "Не знаю", либо называют цвет.
1) Докажите, что кто-то из мудрецов назовет цвет.
2) Докажите, что назовут цвет не менее четырех мудрецов.
Задача Д51*. Двадцати мудрецам принесли 10 белых и 50 черных колпаков. Затем им завязали глаза и надели каждому на голову по черному колпаку, а все ненадетые колпаки спрятали. После этого им развязали глаза и стали у каждого по очереди спрашивать, какого цвета колпак у него на голове. Какой по счету мудрец сможет назвать цвет? Что будут говорить следующие?
Задача Д52*. Султан пригласил шестерых мудрецов в комнату с тремя дверьми: белой, красной и синей – и достал 4 белых, 3 красных и 2 синих колпака. Мудрецы сели в круг и крепко зажмурились. После этого султан надел троим мудрецам белые колпаки, двоим красные и одному синий. Открыв глаза, мудрецы получили возможность видеть цвета колпаков у всех остальных, но не у себя. Каждую минуту раздается удар гонга, после которого все мудрецы, знающие цвет своего колпака, должны выйти в дверь соответствующего цвета. Сколько мудрецов смогут покинуть комнату?
Мудрецы и числа
Задача Д53. Каждому из двух мудрецов дали бумажку с написанным на ней натуральным числом и сообщили, что одно число вдвое больше другого. Когда мудрецы посмотрели на числа, между ними состоялся такой диалог:
А: "Я не знаю твое число".
Б: "И я не знаю твое число".
А: "И я не знаю твое число".
…
Докажите, что рано или поздно кто-то из мудрецов сможет сказать: "Теперь я знаю твое число".
Задача Д54*. Султан вызвал 10 умнейших своих мудрецов и огласил правила нового испытания. Каждому мудрецу сообщат число от 1 до 1000 включительно, одно из чисел строго больше остальных. Затем каждого мудреца по очереди будут спрашивать, не у него ли максимальное число. Он может ответить "Не знаю" либо "У меня". После ответа "Не знаю" испытание продолжается, вопрос задают следующему мудрецу. Если последний мудрец ответил "Не знаю", вопрос опять задают первому мудрецу и так далее. После ответа "У меня" испытание заканчивается. Если мудрец ответил правильно, всех мудрецов отпускают, если неправильно – всех мудрецов казнят.
Мудрецам запретили не только обмениваться какой-либо информацией во время испытания, но даже договариваться о чем-либо заранее. Испытание началось. Королевский палач сто раз обошел всех мудрецов, и сто раз каждый из них ответил "Не знаю". Наконец, палач в сто первый раз спросил первого мудреца, не у него ли максимальное число.
"У меня!" – ответил мудрец. Конечно, ответ был правильный, всех мудрецов отпустили. Какое число было у первого мудреца?
Задача Д55Ї Математик В предложил математикам А и Б такую загадку:
– Я задумал три попарно различных натуральных числа, произведение которых не превосходит 50. Сейчас я конфиденциально сообщу А это произведение, а Б – сумму задуманных чисел. Попробуйте отгадать эти числа.
Узнав произведение и сумму соответственно, А и Б вступили в диалог:
А: "Я не знаю этих чисел, но если бы мое число было суммой, я бы их знал".
Б: "Я все равно не знаю их".
Докажите, что теперь А сможет определить числа.
Задача Д56*. В одиночных камерах сидят 4 друга-математика. Каждому из них сообщили, что их номера в списке различны, двузначны и один из этих номеров равен сумме трех других. Но, даже узнав номера троих других, никто из них не смог вычислить свой номер. Так какие же у них были номера?
Задача Д57*. Каждому из трех логиков написали на лбу натуральное число, причем одно из этих чисел являлось суммой двух других, и сообщили им об этом. Логик не видит, что написано у него на лбу, но видит, что написано у других. Первый логик сказал, что не может догадаться, какое число написано у него на лбу. После этого то же самое сказал второй логик, а затем и третий. Тогда первый сказал: "Я знаю, что у меня на лбу написано число 50". Какие числа написаны у двух остальных?
Решения задач
Занятие 1
1.5. 1) Это не только не высказывание, но и вообще не утверждение. Данное предложение побудительное, а высказывание всегда является повествовательным предложением. Например, "Все умные люди перед тем, как что-либо отрезать, проводят семикратные измерения". Истинность такого высказывания весьма сомнительна.
2) Грамматическая структура этого предложения слишком сложна. При желании можно превратить поэтическую истину в аналогичное по смыслу ложное высказывание "Для того чтобы жить в доме, достаточно его нарисовать". Только зачем?
3) Чтобы превратить это утверждение в высказывание, надо точно указать время и место.
1.7. 1) Да. 2) Нет. Митя и Андрей могут иметь одинаковый рост.
1.8. 1) Достаточно ли заменить дальнюю дорогу на ближнюю? Нет, поскольку завтра королю вообще может быть не суждено никакой дороги. Можно поставить перед глаголом частицу "не": "Завтра королю не выпадает дальняя дорога". Или сказать так: "Завтра королю либо выпадает ближняя дорога, либо вообще не выпадает дороги".
2) Использование антонима ("У него деньжонок мало") вновь приводит к ошибке: денег у него может и вовсе не быть. Спасительное "не" не спасает. Правильное отрицание звучит так: "У него деньжонок мало или совсем нет"
3) Тут все ясно. Любовь либо есть, либо ее нет. Отрицание: "Я денежки не люблю".
1.9. 1) Если контроль за прическами есть, то красить волосы нельзя. Если его отменят, то можно. Но директор возражает против отмены – значит, все же нельзя.
Ответ. Нельзя.
Комментарий. Это утверждение является двойным отрицанием (другими словами, отрицанием отрицания). Истинному утверждению соответствует ложное отрицание и снова истинное двойное отрицание.
2) Если контроль за прическами есть, то красить волосы нельзя. Если решили его запретить, то можно. Если это решение отменить, то снова нельзя. Но директор возражает против отмены – значит, все же можно.
Ответ. Можно.
Комментарий. Здесь отрицание встречается трижды (возражает, отмена, запрет) – т. е. нечетное число раз. Так как пары отрицаний "нейтрализуют" друг друга, то можно считать, что контроль просто отрицается.
1.10. Решение 1. Если бы данное высказывание было истинным, этот критянин был бы лжецом и не мог делать истинных утверждений. Если оно ложное, противоречия нет: этот критянин лжет, но на острове есть другие критяне, которые говорят правду.
Ответ 1. Ложно.
Решение 2. Как доказано в первом решении, эта фраза не является истинным высказыванием. А теперь представьте, что фразу "Все критяне лжецы" сказали все критяне одновременно (например, что говоривший – единственный житель острова). Если это ложное высказывание, то все критяне солгали, что делает каждое высказывание истинным.
Ответ 2. Фразу "Все критяне лжецы", сказанную критянином, вообще нельзя считать высказыванием и обсуждать ее истинность.
Комментарий. В задаче изложен парадокс Эпименида – вариант знаменитого парадокса лжеца. Считается, что греческий философ Филит Косский умер от истощения и бессонницы, пытаясь его разрешить. Чтобы не последовать его примеру, мы избрали простейший путь – исключили из рассмотрения утверждения, говорящие о своей истинности. Более сложная точка зрения изложена в главе о парадоксах книги Рэймонда М. Смаллиана "Как же называется эта книга?".
1.11. 1) Верно отрицание: "Сумма двух двузначных чисел может не быть двузначной". В ошибочности формулировки отрицания "Сумма двух двузначных чисел – не двузначное число" поможет убедиться закон исключенного третьего.
2) Утверждение верно. Его отрицание – "Сумма двух четных чисел может не быть четным числом". Ребята скорее всего скажут "Сумма двух четных чисел может быть нечетным числом". Признаем и такую формулировку допустимой, считая заранее известным, что сумма целых чисел – целое число и что все целые числа либо четные, либо нечетные.
3), 4) Для получения отрицания достаточно заменить "можно" на "нельзя" или "невозможно". В пункте 3 верно утверждение. Например, можно сторону 20 разделить на 4 равных части, а сторону 15 – на 5 равных частей и провести через точки деления прямые, параллельные сторонам. В пункте 4 верно отрицание: площадь исходного квадрата нечетна, а предполагаемых частей – четна.
5) Пусть в школе n учеников. Каждый может иметь от 0 до n – 1 друга – всего n вариантов. Но все эти варианты одновременно реализоваться не могут: если у кого-то n – 1 друг (т. е. он дружит со всеми остальными учениками), то никто другой не может вообще не иметь друзей. Поэтому вариантов меньше, чем учеников, и какой-то вариант соответствует хотя бы двум ученикам.
6) Для формулировки отрицания убрать "не" недостаточно. Если уточнить: "Через любое отверстие…", то ясно, что это общее высказывание, к которому отрицание строится так: "В листке из школьной тетради можно прорезать такое отверстие, через которое может пролезть человек". С такими высказываниями мы еще встретимся на втором занятии. Как ни странно, верно именно отрицание. На рис. 21 показано, как вырезать подходящее отверстие. Чем чаще разрезы, тем более длинная и узкая "змейка" будет его ограничивать.
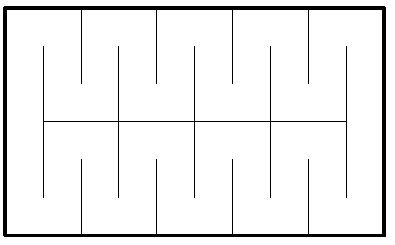
Рис. 21
Занятие 2
2.9. 1) Да, могут. Если все грибы съедобны. 2) Да, могут. Если в корзине есть и съедобные, и несъедобные грибы. 3) Да, могут. Если съедобных грибов вообще нет.
2.10. Нет, не является. Эти высказывания вполне могут выполняться одновременно.
2.11. Иллюстрации изображены на рисунке 22. Одинаковый смысл имеют третье и четвертое высказывания.
2.12. Денис не прав. Он путает высказывания "У всех великих людей плохой почерк" и "Все люди с плохим почерком– великие" (см. рис. 23).
2.13. Правду сказали все трое.
Комментарий. "Хотя бы один" означает "Ровно один или больше одного". В данном случае у Зайца "хотя бы один" означает "ровно один", у Волка – "двое", у Лисы – "все трое".
2.14. "Некоторые врачи имеют недостаточный опыт. Каждый врач хоть когда-нибудь ставил неправильный диагноз. Некоторые врачи опаздывают на работу. Некоторые пациенты недовольны лечением. Некоторые пациенты жалуются на бытовые условия. Никто не выздоравливает за один день".
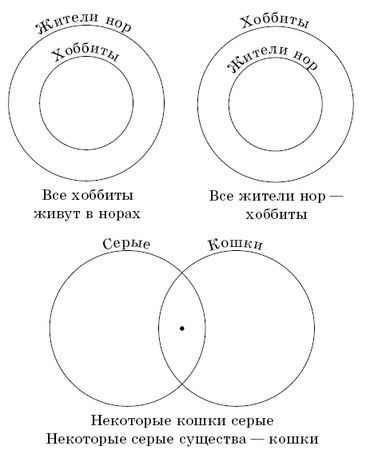
Рис. 22