В евклидовом пространстве E проведём через некоторую точку O все k-мерные ориентированные плоскости размерности k и обозначим через H(k, l) многообразие, составленное из этих плоскостей. В каждой точке x многообразия M проведём касательную к нему плоскость Тх. Обозначим через T(x) плоскость из многообразия H(k, l), параллельную плоскости Tx. Таким образом, возникает отображение T многообразия M в многообразие H(k, l). Это отображение я назвал тангенциальным отображением. Для многообразия H(k, l) я нашёл все циклы с точностью до гомологии. Если Z - некоторый цикл из H(k, l), то он высекает на многообразии T(M) некоторый цикл Y, прообраз которого Q в многообразии М и называется характеристическим циклом. Очень легко доказывается, что характеристические циклы не зависят от числа l при достаточно большом l и являются инвариантами гладкого многообразия M. Здесь имеются, конечно, в виду циклы с точностью до гомологий, т.е. классы гомологий, поэтому в дальнейшем они стали называться классами Понтрягина, а не циклами. В дальнейшем характеристические классы стали предметом изучения многих математиков и играли большую роль в топологии. Первая же важная проблема, которая связана с ними, заключается в следующем: легко доказывается, что характеристические классы являются инвариантами гладкого многообразия M; возникает вопрос, не являются ли они инвариантами самого топологического многообразия M? Эту задачу я пытался решить, но не сумел.
Много лет спустя С. П. Новиков доказал, что если рассматривать характеристические классы над полем рациональных чисел, то они являются инвариантами топологического многообразия M, т.е. не зависят от введённой на нём гладкости. Характеристические классы конечного порядка, напротив, не являются инвариантами топологического многообразия M. Это было установлено и сыграло также существенную роль для решения некоторых важных задач. В частности, это обстоятельство было использовано для доказательства того, что на топологической сфере можно ввести различные гладкости, не эквивалентные между собой.
Связь между гомотопической классификацией отображений сферы S на сферу S и теорией гладких многообразий была установлена мною отнюдь не в 1936 году, а гораздо позже, когда я старался упростить доказательство, которое для k=1, 2 первоначально было чудовищно сложно, а также старался решить задачу классификации отображений для k≥3. Мне кажется, что характеристические циклы были построены мною ещё до войны, но первая публикация была дана только в 1942 году 14. Существенно упростить решение задачи для k=1 и k=2 мне удалось. Решить задачу для k≥3 не удалось, несмотря на все мои усилия.
Попытки решить эту задачу продолжались несколько лет. Точно так же несколько лет я занимался гладкими многообразиями, в частности оснащёнными, а также характеристическими классами.
Эта деятельность была закончена мною в начале 50-х годов и завершилась чтением курса лекций на эту тему. Затем была опубликована монография "Гладкие многообразия и их применения в теории гомотопий" в 1955 г. в "Трудах Математического института".
Несмотря на то, что я не сумел решить задачу для k≥3, результаты, полученные мною по теории гладких многообразий, оказались существенными и вошли в топологию гладких многообразий. Независимо от меня задачей классификации отображений S на S занимался Лере, но совершенно на другом пути. Его первоначальные публикации, подводящие к решению этой проблемы, были крайне формалистичны, и совершенно не видно было, к чему они ведут. Так что я только попытался их изучить, а потом бросил.
В конечном счёте Лере на своём пути решил задачу классификации отображений сферы Sна сферу S при произвольном k. Этим самым моя многолетняя работа в этой области была мною закрыта. Это послужило одной из причин, по которым я полностью бросил топологию и занялся прикладными проблемами. Впрочем, для этого были и более существенные причины. Об этом, однако, я расскажу позже.
* * *
Математик не скажет: "Я работал", он скажет: "Я занимался". Это значит, он занимался математикой. Может быть, читал математическую работу, может быть, старался доказать новую теорему, может быть писал собственную работу, излагая уже полученные результаты. Обо всём этом говорится: "занимался".
Иногда мне задают вопрос: в чём состоит кухня математического творчества, или иначе: в чём заключается кухня математических занятий, т.е. как получаются новые математические результаты. Полноценного ответа на этот вопрос, я думаю, дать нельзя. Один из героев А. С. Пушкина ("Египетские ночи") говорит: "Всякий талант неизъясним". Подражая Пушкину, можно было бы сказать: процесс математического творчества неизъясним.
Стараясь объяснить процесс научного творчества, Пуанкаре относил значительную часть его на подсознательную деятельность мозга. Делая это, он тем самым отказывался от ответа на вопрос, так как подсознательная деятельность мозга не наблюдаема. Всё же я думаю, что кое-что о процессе математических занятий сказать можно, и постараюсь это сделать.
Главная часть математических занятий заключается в получении новых математических результатов. Математические результаты я делю на два различных типа:
*1*. Математический результат предвидится и формулируется заранее, почти без всяких занятий, а занятия должны дать ответ на вопрос: верен ли формулируемый результат или не верен. То есть здесь имеется лишь два возможных ответа: да или нет.
*2*. Математический результат нельзя предвидеть заранее без всякого научного исследования. Математик имеет дело с какой-то задачей или явлением и ответа заранее предвидеть не может. Его нужно найти. Это и будет результат. В этом случае результат представляет собой совершенно новое математическое явление, или, иначе говоря, новую картину, которую нужно найти, одновременно убеждаясь в том, что она правильна и даёт решение поставленной задачи.
Для результата 1-го типа главный интерес, как правило, заключается в его доказательстве, а не в формулировке. Для результата 2-го типа интересна формулировка, а не только доказательство. Мне лично гораздо больше нравятся результаты 2-го типа. Приведу классические образцы результатов 1-го и 2-го типов.
Результат 1-го типа: проблема Гольдбаха. Ещё в XVIII столетии петербургский академик Гольдбах сформулировал следующую теорему: каждое чётное число может быть представлено как сумма двух простых чисел. Проблема Гольдбаха заключается в том, чтобы дать ответ на вопрос, правильна ли эта теорема или неправильна.
Проблема Гольдбаха до сих пор не решена. Ослабленная проблема Гольдбаха была решена И. М. Виноградовым в 1937 году. Она заключается в следующем. Легко видеть, что если теорема Гольдбаха верна, то каждое нечётное число можно представить в виде суммы трёх простых чисел. Однако из этой теоремы не следует теорема Гольдбаха. Когда говорят, что Виноградов решил проблему Гольдбаха, то имеют в виду данное им доказательство теоремы о том, что всякое нечётное число можно представить в виде суммы трёх простых чисел. Доказать теорему Гольдбаха очень трудно, так как в ней увязываются аддитивные и мультипликативные свойства целых чисел, кроме того, трудность видна также из того, что она до сих пор не поддаётся решению, а решена только частично и то с огромным трудом. Заслуга Виноградова заключается не столько в том, что он решил ослабленную проблему Гольдбаха, а в том, что он создал новый метод - метод тригонометрических сумм, позволивший ему решить ряд теоретико-числовых проблем. В частности, ослабленную проблему Гольдбаха.
Результат 2-го типа. Предельные циклы Пуанкаре. Если состояние технического или физического объекта определяется двумя величинами x, y, то процесс изменения этих величин во времени обычно описывается системой двух обыкновенных дифференциальных уравнений dx
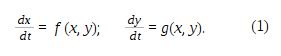
Здесь правые части уравнений не зависят от времени t, т.е. система (1) автономна. Систему дифференциальных уравнений (1) можно интерпретировать на плоскости в виде векторного поля, ставя в соответствие каждой точке (x, y) плоскости фазовый вектор ( f(x, y), g(x, y)). Решение системы (1) можно также интерпретировать в виде линии на той же фазовой плоскости. Для этого проводят линию, описываемую решением (x(t), y(t)) на фазовой плоскости, считая t параметром. Эти линии называются фазовыми траекториями системы (1). Они не пересекаются между собой, покрывают всю плоскость и дают так называемую фазовую картину решений системы дифференциальных уравнений (1). Две эти интерпретации связаны между собой. Фазовой вектор, отнесённый к точке (x, y), касается фазовой траектории, проходящей через эту точку.
Если задано начальное значение (x0, y0) при заданном значении времени t0, то, конечно, можно вычислить решение системы уравнений (1) при этом начальном значении на любом конечном отрезке времени t0 ≤ t ≤ t1. Возможность нахождения численного решения дают современные вычислительные машины. Но нахождение таких решений на конечном отрезке времени не решает всех проблем, которые возникают относительно системы дифференциальных уравнений (1). Так, вопрос о том, имеет ли система уравнений (1) периодические решения, т.е. замкнутые фазовые траектории, решить, вычисляя решения на конечных отрезках времени, невозможно. Точно так же невозможно решить вопрос о том, как ведут себя траектории, когда время неограниченно возрастает, а это очень важно для разных технических вопросов. На всё это обратил внимание Пуанкаре, введя в рассмотрение фазовую картину системы дифференциальных уравнений (1), положив этим начало качественной теории дифференциальных уравнений.
Пуанкаре принадлежит основное понятие, возникшее в качественной теории, - понятие предельного цикла. Периодическое решение системы (1) изображается на плоскости в виде замкнутой фазовой траектории. Если вблизи неё нет других замкнутых траекторий, то эта замкнутая фазовая траектория называется предельным циклом. Оказывается, что фазовые траектории, проходящие вблизи предельного цикла, наматываются на него как спирали и изнутри, и снаружи, при неограниченном возрастании или убывании времени t. В предположении некоторой общности положения оказывается, что траектории на предельный цикл снаружи и изнутри наматываются в обоих случаях либо при возрастании t, либо при убывании времени t. Если они наматываются при возрастании времени t, то предельный цикл является устойчивым решением. Физический прибор, описанный системой (1), может работать на этом предельном цикле, т.е. выдавать устойчивые периодические колебания. Пуанкаре обратил внимание также на значение положения равновесия системы (1), т.е. таких точек фазовой плоскости, которые обращают в нуль правые части дифференциальных уравнений (1). Эти точки являются постоянными решениями системы (1). Поведение траекторий вблизи них играет важную роль. Оно было изучено Пуанкаре, и он дал классификацию положений равновесия на основании этого поведения.
Качественная теория системы уравнений (1), построенная Пуанкаре, является характерным результатом 2-го типа. Ясно, что очень важно было решить систему уравнений (1), но получить её решение в виде формул удаётся лишь для очень немногих систем уравнений. Поэтому возникла задача найти какой-то новый подход к рассмотрению этих уравнений. Это сделал Пуанкаре, сосредоточив своё внимание на фазовой картине траекторий. Он извлёк из этой фазовой картины то важнейшее, что она даёт. Это предельные циклы, положения равновесия и общий характер поведения траекторий при неограниченно возрастающем t. Таким образом, было обнаружено новое математическое явление, предвидеть которое исходя из системы (1) невозможно.
В 30-х годах этого столетия предельные циклы Пуанкаре нашли применение в радиотехнике. А именно, А. А. Андронов показал, что ламповый генератор работает на предельном цикле. До этого работу ламповых генераторов пытались объяснить при помощи линейных дифференциальных уравнений, что было, конечно, невозможно. Качественная теория дифференциальных уравнений, основанная Пуанкаре, получила значительное развитие в работах многих математиков. В частности, Андронов ввёл в связи с фазовой картиной на плоскости понятие грубой системы, важной с физической точки зрения. Я помог ему немного в решении некоторых связанных с этим задач и стал соавтором этого понятия.
Нет сомнений, что при решении ослабленной проблемы Гольдбаха Виноградов преодолел гораздо большие трудности, чем Пуанкаре при геометрическом изучении системы дифференциальных уравнений (1). Несмотря на это, описанный результат Пуанкаре кажется мне гораздо более интересным и важным для математики, чем результат Виноградова. Конечно, это, может быть, объясняется тем, что в достижении Виноградова я не знаю того, что только и может быть в нём интересно, именно самого доказательства. А результат Пуанкаре мне ясен, я умею применять его и знаю применения.
Здесь всплывает на поверхность важнейший для занятия математикой вопрос. Именно, вопрос о выборе тематики. Вопрос о том, чем следует заниматься. Вопрос этот для математиков, быть может, более труден, чем для специалистов других областей знаний. Математика возникла как наука чисто прикладная, и в настоящее время её основной целью является изучение окружающей нас материальной действительности на пользу человечества. С другой стороны, в развитии математики есть своя логика, которая часто уводит в сторону от прикладного пути. Создаются целые теории, не имеющие отношения к приложениям, но чрезвычайно красивые в своём роде. Эти математические красоты доступны только математикам и поэтому не могут быть оправданием для создания таких теорий.
Но всё же теории, не имеющие приложения, а имеющие большую внутреннюю стройность, нельзя считать незаконнорождёнными и отвергать. Они составляют внутреннюю ткань всей математики, и их иссечение могло бы нарушить её целостность. Кроме того, известны случаи, когда первоначально лишённые всяких приложений понятия находят в дальнейшем свои приложения. Примером могут служить конические сечения. Я лично считаю, что при занятиях математикой часто следует обращаться к первоисточникам, т.е. к её приложениям. Это вносит свежую струю в развитие математики, так как из глубины разума невозможно извлечь ничего столь значительного и интересного, что можно извлечь из прикладных задач. Но всё же, руководствуясь соображениями приложений, хочется выбирать такие математические проблемы, которые сами по себе, как математические, интересны. Такое сделать нелегко, но всё же иногда удаётся.
Существует, однако, совершенно другой подход к математической проблематике. Это стремление решить знаменитые проблемы, т.е. такие, которые давно поставлены, но не поддаются решению. Прекрасными примерами таких проблем являются проблема Гольдбаха и великая теорема Ферма. Но такой подход кажется мне уж очень спортивным, а ведь наука не спорт. Её главной целью является подчинение людям окружающей материальной действительности с тем, чтобы использовать её для жизни людей. Некоторые считают, что, решая трудные проблемы, математики совершенствуют свой аппарат для того, чтобы в дальнейшем его можно было использовать по прямому назначению. Но я полагаю, что лучше уж совершенствовать свой аппарат, употребляя его сразу по прямому назначению для решения сколько-нибудь прилагаемых к жизни задач. Столь же безосновательным мне кажется утверждение, что, играя в шахматы, люди совершенствуют свои умственные способности. Я считаю, что игра в шахматы скорее изнуряет умственные способности. Лучше уж совершенствовать их на чём-то нужном.
При попытке объяснить процесс математического творчества я буду исходить из одного высказывания Пуанкаре, смысл которого состоит в следующем. Всякое, даже очень сложное математическое построение состоит из очень простых логических переходов, каждый из которых не представляет никакой трудности при понимании. Сложное переплетение всех этих простых переходов представляет собой трудную для понимания конструкцию, ведущую к результату.
Таким образом, сложное математическое построение представляет собой как бы логическое кружево из мелких стежков очень простой структуры. На одном конце этого сложного куска кружев находится предпосылка, а на другом - результат. Каждый стежок, составляющий кусок кружев, очень прост. Всё в целом сплетение представляется очень сложным. Для понимания его требуется большой опыт и одарённость математика. Процесс математического творчества заключается в сплетении этого сложного логического куска, на одном конце которого находится предпосылка, а на другом - научный результат.
Как же математик выплетает то сложное кружево, которое ведёт к желанной цели? Для этого он, по моему представлению, намечает сперва узловые точки будущего куска. Для будущего сложного сплетения следует удачно наметить его узловые точки. После того, как эти узловые точки будут намечены, заполнить оставшиеся пустоты будет легче, чем построить кружево в целом. Для простоты будем считать, что всё сложное сплетение, ведущее от предпосылки к результату, представляет собой последовательность логических шагов, которую нужно пройти.