Акторно-сетевой подход сходен с подходом Фуко в том, что касается акцентирования значимости материального. Речь, тела, жесты и материалы – вроде зданий, кораблей, самолетов или огнестрельного оружия – все рассматривается как проявление стратегической логики, все участвует в поддержании всего. Все создано отношениями и участвует в их создании. Отличие же акторно-сетевой теории от постструктуралистского подхода состоит в том, что она менее увлечена "границами возможного", установленными современностью (а в некоторых вариантах и вовсе безразлична к данной проблематике). Вместо этого акторно-сетевая теория изучает конкретные стратегии, рекурсивно и продуктивно встроенные в отношения производства объектов, организаций, субъектов и т. п. ant допускает не один, а множество современных "способов упорядочивания".
Что означает это различие между подходом М. Фуко и акторно-сетевым анализом? Предположим, что объекты действительно представляют собой просто "относительные неопределенности" ("контингентности"). Это означает, что способы их образования и то, как приобретают устойчивость сформировавшие их отношения, – вопрос преимущественно эмпирический. В свою очередь, как подчеркивают теоретики акторно-сетевого подхода, вся совокупность возможностей мира ограничена, но ограничена случайным образом, и поскольку вселенная может явить нам разнообразное множество вещей, способы их упорядочивания не агрегируются в большие эпистемические блоки.
Насколько удачен выбранный нами способ рассуждения? С одной стороны, можно рассматривать вышесказанное как освобождение от мрачной одержимости Фуко границами условий возможного, от его предубеждения против всего, что за последние двести лет незаметно лишило нас свободы посредством логики и стратегии современной эпи-стемы. Однако есть и другая возможность: сказать, что подобное рассуждение – лишь форма слепоты. В таком случае акторно-сетевая теория оказывается вовлеченной в интеллектуальную и политическую борьбу против попыток заглянуть за границы возможного. Найти неоткрытый континент и исследовать затененные, гетеротопичные места – места Иного, которые лежат за пределами сегодняшних возможностей.
Данная работа посвящена этому недостатку "инаковости" (alterity). Мой вопрос таков: что есть объект, если мы начинаем думать об "инаковости" серьезно? Здесь я попробую рассмотреть эту тему пространственно или, вернее, топологически. Во-первых, я настаиваю на том, что производство объектов действительно имеет пространственные следствия; и, далее, что пространство не самоочевидно и не единично, но имеются множественные формы пространственности. Во-вторых, я предполагаю, что использование объектов само создает пространственные условия возможности и невозможности. Пространственности порождаются и приводятся в действие расположенными в них объектами – именно этим определяются границы возможного. (Следуя первому утверждению, стоит упомянуть, что пространственные возможности по своему характеру также множественны.) Существуют различные формы пространственностей; те, о которых говорим мы, включают в себя регионы, сети и потоки. В-третьих, я предполагаю, что эти пространственности и объекты, которые заполняют и создают их, плохо совместимы, т. е. находятся в напряженных отношениях. Они Иные по отношению друг к другу. Объектность есть отражение и творение их несовместности, результат переключения различных пространственных возможностей.
Португальцы
В исследованиях, посвященных "науке, технике и обществу" (STS studies), теоретический анализ, как правило, опирается на рассмотрение ряда эмпирических примеров. Для нужд своего анализа мы обратимся к примеру одного крупномасштабного и весьма заметного исторического явления – технологиям португальской колониальной экспансии.
Как известно, иберийские морские технологии – новые корабли и новые практики навигации – играли ключевую роль в колониальном доминировании Европы. Христофор Колумб добрался до Центральной Америки в 1492 году, Васко да Гама достиг берега Индии в 1498. Описание кораблей, использовавшихся в ранние периоды экспансии, позволяет выделить несколько технических особенностей. Эти суда были удобны в управлении (маленькие корабли быстро переоснащались при смене ветра); относительно защищены от абордажа (даже если атакующим удавалось забраться на борт, их встречал смертоносный огонь из укрытий на носу и корме); автономны (благодаря передовым навигационным технологиям, которые позволяли кораблям удаляться на значительное расстояние от земли и пользоваться всеми преимуществами попутных ветров и течений), а также обладали существенными транспортными возможностями и обслуживались немногочисленными командами (то есть, в отличие от гребных кораблей, могли оставаться в море месяцами).
Таким образом, в картине ранней португальской и испанской экспансии особое место занимают огромные корабли – галеоны – уходящие в море, проводящие в плавании до восемнадцати месяцев, возвращающиеся (если возвращающиеся) с грузом специй или награбленного золота. "Если" – потому что, несмотря на успех этих новых морских технологий, с их оригинальными кораблями и приспособленными к новым условиям навигационными техниками, корабли тонули, терялись или их команды умирали от голода и тропических болезней. Как говорили португальцы: "Если хочешь научиться молиться – отправляйся в море".
Акторно-сетевая теория об объектах
С точки зрения акторно-сетевой теории описанная выше технология представляет собой сеть, причем сетевой анализ применим к различным уровням ее изучения. Например, корабль может быть представлен в виде сети – сети остовов, рангоутов, парусов, канатов, пушек, складов продовольствия, кают и самой команды. С другой стороны, при более обобщенном рассмотрении, навигационная система, со всеми ее эфемеридами, астролябиями и квадрантами, таблицами расчетов, картами, штурманами и звездами, также может быть рассмотрена как сеть. Далее, при еще более отстраненном анализе, вся португальская имперская система в целом, с ее портами и пакгаузами, кораблями, военными диспозициями, рынками и купцами, может быть описана в тех же категориях.
Выше было упомянуто множество объектов. Аргумент акторно-сетевой теории таков: объект (например, корабль) остается объектом до тех пор, пока отношения между ним и связанными с ним объектами устойчивы и все сохраняется на своих местах. Штурманы, противники-арабы, ветра и течения, команда, складские помещения, орудия: если эта сеть сохраняет устойчивость, корабль остается кораблем, он не тонет, не превращается в щепки, напоровшись на тропический риф, не оказывается захваченным пиратами и уведенным в Аравийское море. Он не пропадает, не теряется до тех пор, пока команда не сломлена болезнями или голодом. Корабль определяется своими отношениями с другими объектами и акторно-сетевой анализ направлен на исследование стратегий, которые производят (и, в свою очередь, произведены) этой объектностью, синтаксисом или дискурсом, определяющими место корабля в сети отношений.
Брюно Латур предложил интересную версию этой истории. Он говорит о неизменных мобильностях (Latour, 1990). Корабли представляют собой "мобильности", потому что действительно происходит их перемещение из Лиссабона в Калькутту. А "неизменные" они потому, что сохраняют при этом перемещении свою форму как сетевые единства. Таким образом, сетевая метафора действует в двух направлениях, на двух уровнях анализа, упомянутых выше. Неизменные мобильности, будучи объектами, сами являются сетями, ансамблями отношений. Но они также включены в сеть отношений с иными объектами. Если эта сеть разрывается, корабль перестает быть кораблем, теряет свою сетевую форму, превращаясь во что-то другое.
Введение в топологию
Все вышесказанное – пример классического акторно-сетевого анализа. Менее привычна другая идея: конституирование объектов с необходимостью предполагает включение пространственных отношений. Латуровский термин "неизменные мобильности" отсылает к понятию движения – движения через пространство. Мы еще вернемся к этому позже. Пока же отметим, что идея сети (или существования объектов как сетевых единств) пространственно не нейтральна и указывает на производство определенного типа пространства. Чтобы прояснить этот аргумент нам потребуется краткое отступление в топологию.
Топология – отрасль математики, изучающая характер объектов в пространстве. Как она работает на практике? Нематематический ответ состоит в том, что топологи изучают пространственность с точки зрения непрерывности фигур. Фигуры сохраняют свойство непрерывности, даже будучи деформированными. В топологии, например, утверждается, что фигура сохраняет непрерывность своей формы, если она сплющена, согнута или растянута, но не в том случае, если она разорвана или сломана. При разрыве или повреждении поверхности она трансформируется, то есть не является более гомеоморфной. Например, топологически куб тождественен сфере, они гомеоморфны. Однако обе эти фигуры принципиально отличаются от фигуры бублика, потому что бублик можно получить из шара или куба, лишь проделав в них отверстие. В двумерном пространстве окружность и квадрат гомеоморфны, но отличны от дуги – чтобы получилась дуга, линию, образующую окружность (или квадрат), нужно разрезать.
Приведенные примеры согласуются с тем, что говорит о пространстве европейско-американский здравый смысл: пространство по характеру своему географично, евклидово. Но это обманчивое ощущение, потому что евклидова геометрия описывает лишь одну из пространственных возможностей. Топологи создают и исследуют разные вероятные пространства или (что, впрочем, одно и то же) различные условия, в которых объекты могут быть деформированы без повреждений. Конвенциональный характер этого вопроса станет более очевидным, если мы обратимся к примеру на Рис. 1.
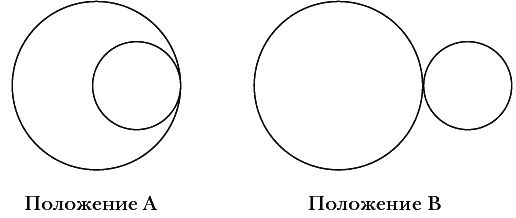
Рисунок 1. Гомеоморфное или не гомеоморфное преобразование?
Топологически две эти формы не эквивалентны. Потому что если мы захотим преобразовать Положение А в Положение В, нам будет недостаточно одной лишь деформации. Нам придется разрезать большую окружность, чтобы вытащить меньшую "наружу". Следовательно, непрерывность бо льшей окружности будет нарушена, а гомеоморфизм – потерян. Однако это верно лишь в том случае, если мы мыслим в двумерном пространстве и вынуждены проводить свои преобразования на плоскости. Если же мы не ограничены двумя измерениями, то достаточно перекинуть одну окружность через другую в точке их соприкосновения, и Положение А будет преобразовано в Положение В без утраты гомеоморфизма. Непрерывность объекта не пострадает.
Приведенный пример иллюстрирует два интересующих нас аспекта проблемы: во-первых, он показывает, что пространственность – это конвенция; во-вторых, что для адекватного ее описания одной евклидовой геометрии мало. Кроме того, пример с окружностями показывает, как тесно связаны между собой вопросы пространственности и непрерывности объектов. При каких обстоятельствах объект может быть изменен (например, перемещен в пространстве относительно прочих объектов) без трансформации его формы? Этим вопросом занимается топология, как область математики, призванная исследовать способности различных фигур к трансформациям (и различные пространства, которые делают эти трансформации возможными). Соответственно, существует множество способов определения того, что будет считаться непрерывностью формы, и что – пространством.
Евклидово и неевклидово пространство, или "Что такое корабль"?
Как мы отметили выше, для европейско-американского здравого смысла наиболее очевидной формой пространства является пространство евклидово. Фигура здесь мыслится как нечто помещенное в систему координат, образованную тремя ортогональными осями, а объект полагается неизменным, если его координаты в трехмерном пространстве остаются постоянными относительно друг друга. Изменение – например, перемещение объекта с одного места на другое, перемещение относительно других объектов – не означает утраты гомеоморфизма, если только отношение координат остается прежним. Так, корабль остается тем же самым кораблем, если, плавая по морям, сохраняет свою форму как физическое тело. Однако акторно-сетевая теория работает с другой, гораздо менее очевидной формой пространственности. Зададимся вопросом: что составляет непрерывность формы объекта как сетевого единства? Объект остается тем же самым объектом, пока сохраняет свое место в устойчивой сети отношений с другими вещами. Следовательно, ответ на данный вопрос: стабильность порядка отношений. Чтобы можно было показать пальцем на объект и сказать: "это корабль" (причем, корабль нормально функционирующий): корпус, парус, мачта, снасти, руль, цейхгауз, команда, вода, ветер – все это и многое другое должно сохранять свои функциональные связи. Все части должны быть на "своих местах" и делать свою работу. На языке акторно-сетевой теории можно сказать, что все элементы должны быть "включены" (enroll) и оставаться "включенными". Так что нормально функционирующий корабль заимствует силу ветра, легкость течения, энергию команды и все это заключает в себе самом.
Обратите внимание: в евклидовом пространстве корабль есть устойчивая совокупность ортогональных координат, описывающих положение кормы, носа, киля, мачты и парусов относительно друг друга; пока корабль плывет, все эти части образуют единое целое. В пространстве сетей корабль также представляет собой устойчивый и непрерывный объект, "сетевую форму", целостность которой зависит от позиций всех релевантных, связанных с ним объектов. Так поддерживается объектная сущность судна. Это означает, что корабли пространственно или топологически множественны, т. е. находятся одновременно и в евклидовом пространстве и в пространстве сетевых отношений. Корабли гомеоморфны в каждом из пространств, поскольку сохраняют свою форму в обоих: физически – в одном, функционально или синтаксически – в другом. Однако перемещаются эти объекты лишь в евклидовом пространстве, в пространстве сетей они неподвижны. Никакого изменения отношений между компонентами, образующими корабли как объекты, не происходит. А если происходит, значит, что-то не так, значит, их сетевая форма "разорвана". В то же время, именно неподвижность корабля в сетевом пространстве делает возможным его перемещение в пространстве евклидовом, позволяя ему без повреждений покрывать расстояние между Калькуттой и Лиссабоном.
Такова анатомия латуровского понятия "неизменной мобильности". Неизменность здесь относится к сетевому пространству, тогда как мобильность – атрибут пространства евклидова. Резюмируя, можно сказать, что объекты способны к перемещениям благодаря своей топологической комплексности, благодаря тому, что они существуют одновременно в различных пространственных системах и потому что произведены они как пересечения этих пространственностей. Забегая вперед и рискуя сделать чрезмерно поспешный вывод, уточним данное нами выше определение объекта: объекты представляют собой пересечения характеристик неизменности формы в разных топологиях.
Создание пространственности
Европейско-американскому здравому смыслу свойственно ощущение "вечного евклидова пространства" – кажется, что пространство предшествует объектам и определяет условия их возможности. Мы чувствуем, что пространство появилось задолго до нас, что оно представляет собой нейтральный "контейнер" внутри которого нашим телам (или португальским кораблям) приходится существовать. Отчасти это так. Без сомнения существуют отдельные пространственные конфигурации, предшествующие некоторым объектам в евклидовом пространстве. Но, как мы отмечали выше, в топологии вопросы пространственности и гомеоморфизма объектов неразрывно связаны. Действительно, топологически объекты и пространства созданы вместе. Изобретая объекты и определяя, что в их случае будет считаться неизменностью формы, топология вместе с тем изобретает и определяет пространственные условия их возможности. Однако мы можем развить этот аргумент и за пределами топологии. Объект из нашей повседневной жизни, сформированный, деформированный или перемещенный с сохранением непрерывности формы в евклидовом пространстве в то же время создает это пространство. Или, если сформулировать данный тезис более общо и лаконично, пространства сделаны с использованием объектов.