Конечно, это была удобная возможность сделать новое предсказание: если бы вы могли измерить расстояние до звезд, вы нашли бы их, фактически, намного более удаленными, чем планеты. Если бы это было возможно во времена Бруно, он мог бы спастись от огня. Но это было за столетия до того времени, когда расстояние до звезд смогло быть измерено. С практической точки зрения то, что сделал Бруно, было формулирование утверждения, которое было не проверяемо при заданной технологии того времени. Предположение Бруно легко устанавливало звезды на таком расстоянии, что никто не мог бы проверить его идею.
Так что иногда необходимость объяснить, как вещи объединяются, заставляет вас постулировать новые гипотезы, которые вы просто не можете проверить. Это, как мы видели, не означает, что вы ошибаетесь, но это означает, что основатели новых унификаций могут легко оказаться на зыбком грунте.
На деле может быть еще хуже. Такие гипотезы имеют обыкновение зацепляться друг за друга. Фактически, Копернику нужно было, чтобы звезды были очень удаленными. Если бы звезды были так близко, как верил Аристотель, вы могли бы опровергнуть движение Земли – поскольку, если Земля движется, наблюдаемые положения звезд друг относительно друга менялись бы. Чтобы объяснить, почему этот эффект не виден, Коперник и его последователи поверили, что звезды очень далеко. (Конечно, мы знаем теперь, что звезды тоже двигаются, но они находятся на таких чудовищных расстояниях, что их положения в нашем небе изменяются экстремально медленно.)
Но если звезды столь далеки, как мы можем их видеть? Они должны быть очень яркими, вероятно, столь же яркими, как и Солнце. Поэтому предположение Бруно о вселенной, заполненной бесконечно большим числом звезд, естественно подходит к предположению Коперника, что Земля движется как планета.
Мы видим здесь, что различные предложения по унификации часто идут вместе. Предположение, что звезды объединяются с Солнцем, идет вместе с предположением, что планеты объединяются с Землей, и оба этих предположения требуют, чтобы движение и покой были объединены.
Эти идеи, новые в шестнадцатом столетии, противоположны другой группе идей. Предположение Птолемея, что планеты объединяются с Солнцем и Луной и что все они двигаются по эпициклам, шло рука об руку с теорией движения Аристотеля, которая объединяла все известные явления на Земле.
Итак, мы достигли двух групп идей, каждая из которых содержит несколько предположений по унификации. Следовательно, на кону часто оказывается целая группа идей, в которых различные вещи унифицируются на различных уровнях. Перед тем, как споры разрешаются, имеются хорошие основания для уверенности с каждой стороны. Каждая сторона может поддерживаться наблюдениями. Иногда даже один и тот же эксперимент может быть интерпретирован как доказательство конкурирующих теорий унификации.
Чтобы увидеть, как это может происходить, рассмотрим мяч, падающий с вершины башни. Что происходит? Он падает на землю и приземляется у основания башни. Он не улетает в западном направлении. Ну, вы могли бы сказать, что Коперник и его последователи, очевидно, ошиблись, опыт доказывает, что Земля не вращается вокруг своей оси. Если бы Земля вращалась, мяч приземлился бы весьма далеко от основания башни.
Но Галилей и Ньютон могли бы также заявить, что падение мяча доказывает их теорию. Принцип инерции говорит нам, что если мяч движется в западном направлении вместе с Землей, когда он сброшен, он будет продолжать двигаться на запад и в процессе падения. Но мяч двигается на запад точно с той же скоростью, что и башня, так что он падает к основанию башни. То же самое доказательство, которое аристотелев философ мог бы использовать для подтверждения, что Галилей ошибся, принимается Галилеем как доказательство, что его теория корректна.
Как же нам, тем не менее, различить, какое предложенное объединение правильно, а какое ложно? В некотором смысле, тут имеется преобладание доказательства. Одна гипотеза оказывается настолько более плодотворна, чем другая, что рациональная личность не будет иметь выбора, кроме как согласиться, что первая доказана. Что касается ньютоновской революции, то тут, по существу, было реальное доказательство из наблюдения, что Земля движется относительно звезд. Но перед тем, как это произошло, точность ньютоновских законов была доказана в таком большом количестве инстанций, что тут не могло быть поворота назад.
Однако, в середине научной революции часто имеются рациональные основания, оказывающие поддержку соперничающим гипотезам. Мы находимся сейчас в таком периоде, и мы будем исследовать в последующих главах конфликтующие утверждения по объединению. Я сделаю все от меня зависящее, чтобы объяснить аргументы, которые поддерживают различные стороны, пока буду показывать, почему ученые еще достигают консенсуса.
Конечно, нам надлежит проявлять осторожность. Не все доказательства, высказанные в поддержку взгляда, надежно обоснованы. Иногда утверждения, придуманные в поддержку теории, испытывающей затруднения, являются только ее усовершенствованиями. Я недавно встретился с энергичной группой людей, стоящих в проходе на рейс из Лондона в Торонто. Они поздоровались и спросили меня, откуда я прибыл, и когда я сказал им, что я возвращаюсь с космологической конференции, они немедленно спросили меня про мой взгляд на эволюцию. "О, нет," – подумал я, тогда надо продолжать говорить им, что естественный отбор доказал свою правильность вне всяких сомнений. Они представились как члены Библейского колледжа, возвращающиеся после миссии в Африке, одна из целей которой, как оказалось, заключалась в проверке догматов креационизма. Так как они хотели втянуть меня в дискуссию, я предостерег их, что они проиграют, так как я знаю почти все доказательства. "Нет," – настаивали они, – "вы не знаете все факты." Так что я пошел на это. Когда я сказал: "Но вы, конечно, согласитесь с фактом, что мы имеем ископаемые останки многих созданий, которые больше не живут," – они ответили: "Нет!"
"Почему вы полагаете, что нет? Как насчет динозавров?"
"Динозавры все еще живы и бродят по земле!"
"Это нелепо! Где?"
"В Африке."
"В Африке? Африка полна людей. Динозавры на самом деле громадные. Как получается, что никто их не видит?"
"Они живут глубоко в джунглях."
"Кто-то все равно должен был их видеть. Вы утверждаете, что знаете кого-нибудь, кто их видел?"
"Пигмеи говорили нам, что они видят их каждый раз все время. Мы смотрели, но мы не видели ни одного, но мы видели царапины, которые они сделали, на высоте от восемнадцати до двадцати футов на стволах деревьев."
"Тогда вы согласитесь, что это гигантские животные. И ископаемые останки свидетельствуют, что они жили большими стадами. Как это могло бы быть, что никто, кроме пигмеев, их не видел?"
"Это просто. Они проводят большую часть своего времени в спячке в пещерах."
"В джунглях? В джунглях есть пещеры?"
"Конечно, есть, почему нет?"
"Достаточно большие пещеры, чтобы туда поместился гигантский динозавр? Если пещеры столь велики, их должно быть легко найти, и вы могли бы заглянуть внутрь и увидеть их спящими."
"Чтобы защитить себя во время своей спячки, динозавры закрывают входы своих пещер навозом, так что никто не может сказать, что они здесь."
"Как они так хорошо закрывают свои пещеры, что их нельзя увидеть? Они используют свои лапы или, возможно, пихают навоз своим носом?"
В этом месте креационисты согласились, что они не знают, но они сказали мне, что "библейские биологи" из их школы находятся сейчас в джунглях в поисках динозавров.
"Будьте любезны, дайте мне знать, если они обнаружат хоть одного живого," – сказал я и вернулся на свое сидение.
Я это не выдумал, и я рассказал это не только для вашего развлечения. Это иллюстрирует, что рациональность не всегда является простым упражнением. Обычно рациональным является не верить в теорию, которая предсказывает нечто, что никто никогда не видел. Но иногда имеются веские основания для чего-то быть никогда не наблюдаемым. Как никак, если там есть динозавры, они должны где-то прятаться. Почему не в пещерах в джунглях Африки?
Это может показаться глупым, но физики, занимающиеся частицами, не один раз чувствовали необходимость придумать невидимые частицы, такие как нейтрино, чтобы придать смысл определенным теоретическим или математическим результатам. Чтобы объяснить, почему их тяжело зарегистрировать, они вынуждены были сделать нейтрино очень слабо взаимодействующими. В этом случае это была правильная стратегия, через много лет кто-то оказался в состоянии разработать эксперимент, который нашел нейтрино. И они взаимодействовали очень слабо.
Итак, иногда является рациональным не отбрасывать прочь хорошую теорию, если она предсказывает вещи, которые не могут наблюдаться. Иногда гипотезы, которые вы вынуждены были придумать, оказываются правильными. Придумывая такие специальные (ad hoc) гипотезы, вы не только можете сохранить правдоподобность идеи, но также иногда и предсказать новые явления. Но с некоторого момента вы начинаете перегибать палку. Обитающие в пещерах динозавры, вероятно, квалифицируются именно так. Когда вы проходите точку, где когда-то хорошая идея становится ничего не стоящей, неприятности первыми являются предметом критики. Это определенно тот самый случай, когда хорошо подготовленные, умные люди не соглашаются. Но, в конечном счете, достигается точка, где имеется такой перевес доказательств, что ни одна рациональная, ясно мыслящая персона не будет думать об идее, как о правдоподобной.
Одним из способов оценить, достигли ли вы этой точки, служит взгляд на однозначность. Во время научной революции в каждый момент времени на столе оказываются часто несколько предложений по унификации, угрожая повести науку в несовместимых направлениях. Это нормально, и в середине революции нет необходимости в рациональных основаниях, чтобы выбрать одно среди других. В такое время даже очень умные люди, которые выбирают между соревнующимися взглядами, слишком скоро и часто ошибутся.
Но одно предложение по объединению может завершиться объяснением намного большего, чем остальные, и обычно это простейшее предложение. В этот момент, когда отдельное предложение чрезвычайно превосходит остальные с точки зрения генерирования новых прозрений, согласия с экспериментом, объяснительной силы и простоты, это принимается за видимость однозначности. Мы говорим, что предложение попало в круг истины.
Чтобы увидеть, как это может произойти, рассмотрим три унификации, предложенные одной персоной, немецким астрономом Иоганном Кеплером (1571-1630). На протяжении жизни Кеплера его навязчивой идеей были планеты. Поскольку он верил, что Земля является планетой, он знал их шесть, от Меркурия до Сатурна. Их движения по небу наблюдались тысячи лет, так что было весьма много данных. Самые точные данные пришли от датского астронома Тихо Браге. Кеплер, в конце концов, пришел работать к Тихо Браге, чтобы овладеть его данными (и после смерти Браге он своровал их, но это другая история).
Каждая планетная орбита имеет радиус. Каждая планета также имеет орбитальную скорость. Надо добавить, что скорость не однородна, планеты ускоряются и замедляются, когда они двигаются вокруг Солнца по своим орбитам. Все эти числа кажутся случайными. Кеплер всю свою жизнь добивался принципа, который мог бы объединить движения планет, и, сделав это, объяснить данные по планетарным орбитам.
Сначала Кеплер занялся унификацией планет, лежащей на линии античной традиции, по которой космологическая теория должна использовать только простейшие фигуры. Одна из причин, по которой греки верили в круги, двигающиеся по кругам, заключается в том, что круг есть простейшая, а потому самая прекрасная из замкнутых фигур. Кеплер исследовал не менее прекрасные геометрические фигуры, которые могли объяснить размеры орбит планет. И он нашел очень элегантную идею, проиллюстрированную на Рис.1.
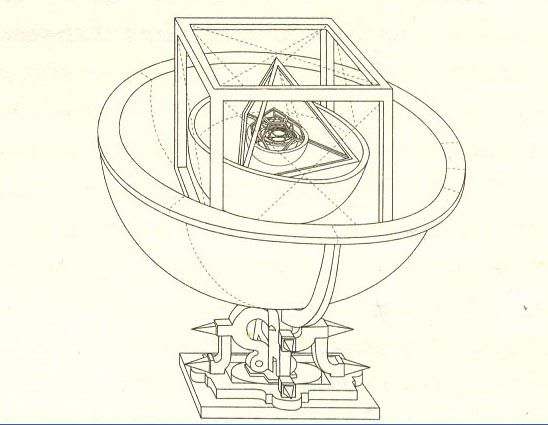
Рисунок 1. Первая теория Солнечной системы Кеплера, основанная на Платоновых телах.
Примем орбиту Земли как данную. Тогда необходимо объяснить пять чисел: пять отношений диаметров орбит других пяти планет к диаметру орбиты Земли. Если они могут быть объяснены, должна существовать некоторая красивая геометрическая конструкция, которая дает в точности эти пять чисел. Не больше и не меньше. Так что же, проблема в геометрии, для которой имеются точно пять ответов?
Да. Куб является совершенным видом тела, для которого каждая сторона такая же, как и любая другая, и каждое ребро имеет ту же длину, что и все остальные ребра. Такие тела называются Платоновыми телами. Сколько их? Точно пять: кроме куба, еще тетраэдр, октаэдр, додекаэдр и икосаэдр.
Кеплеру долго не удавалось сделать ошеломляющее открытие. Впишем орбиту Земли в сферу. Опишем додекаэдр вокруг сферы. Опишем сферу вокруг него. Орбита Марса располагается на этой сфере. Опишем тетраэдр вокруг этой сферы и следующую сферу вокруг тетраэдра. Орбита Юпитера располагается на этой сфере. Вокруг орбиты Юпитера располагается куб, вне которого летает Сатурн. Внутри земной орбиты Кеплер расположил икосаэдр, вокруг которого вращается Венера, а внутри венерианской орбиты расположился додекаэдр, для Меркурия.
Эта объединяющая теория объясняла диаметры орбит планет, что ни одна теория не делала раньше. Это было математически красиво. Так почему в это не поверили? В той же степени, в какой теория была неотразима, она никуда не привела. На ее основе не было предсказано никаких новых явлений. Она даже не привела к пониманию орбитальных скоростей планет. Идея была слишком статической; она объединяла, но не приносила науке ничего интересного.
Кеплер думал об этом долгое время. Поскольку диаметры орбит были объяснены, ему нужно было только объяснить скорости различных планет. Наконец он предположил, что когда планеты путешествуют, их "пение" и частоты нот пропорциональны их скоростям. Высоты пения различных планет, когда они путешествуют по своим орбитам, составляют гармонию шести голосов, которые он назвал гармонией сфер.
Эта идея также имела античные корни, возвращаясь к открытию Пифагора, что корни музыкальной гармонии находятся в отношениях чисел. Но она страдала от очевидной проблемы. Эта идея неоднозначна: имеется много красивых согласований шести голосов. Даже хуже, оказалось, что есть больше, чем шесть планет. И Галилей, современник Кеплера, открыл четыре луны, вращающихся вокруг Юпитера. Так что была еще и другая система орбит в небе. Если теория Кеплера была верна, она должна была быть применима и к вновь открытой системе. Но она была не применима.
Отдельно от этих двух предположений о математической структуре космоса Кеплер сделал три открытия, которые привели к реальному прогрессу в науке. Это были три закона, благодаря которым он сегодня широко известен, предложенные после многолетнего изнурительного кропотливого анализа данных, которые он украл у Тихо Браге. Они были не столь красивы, как другие предложения Кеплера, но они работали. Более того, один из них совершал нечто, чего Кеплер не смог бы сделать иным образом, а именно, было найдено соотношение между скоростями и диаметрами орбит. Три закона Кеплера не только согласуются с данными по всем шести планетам, они согласуются и с наблюдениями спутников Юпитера.
Кеплер открыл эти три закона потому, что он принял унификацию Коперника в свои логические заключения. Коперник сказал, что Солнце находится в центре (или, на самом деле, вблизи центра) вселенной, но в его теории планеты двигались бы тем же образом, было бы Солнце там или нет. Его единственной ролью было освещение сцены. Успех теории Коперника привел Кеплера к вопросу, а не может ли нахождение Солнца вблизи центра каждой планетной орбиты указывать на реальное совпадение центров. И не может ли Солнце, вместо этого, играть некоторую роль в определении планетных орбит. Может ли Солнце некоторым образом оказывать силу на планеты, и может ли эта сила быть объяснением их движения?
Чтобы ответить на эти вопросы, Кеплер выяснил роль точного положения Солнца в каждой орбите. Его первый большой прорыв заключался в открытии, что орбиты не являются кругами, они являются эллипсами. И у Солнца определенная роль: оно находится точно в фокусе эллипса каждой орбиты. Это был первый закон Кеплера. Вскоре после этого он открыл свой второй закон, который заключался в том, что скорости планет на их орбитах возрастают или уменьшаются, когда планеты двигаются ближе к Солнцу или дальше от него. Позднее он открыл третий закон, который управляет отношениями скоростей планет.
Эти законы отметили некоторый глубокий факт унификации солнечной системы, поскольку законы применимы ко всем планетам. Награда заключалась в том, что впервые мы имели теорию, которая могла делать предсказания. Предположим, открыта новая планета. Можем ли мы предсказать, какой будет ее орбита? До Кеплера никто бы не смог. Но, имея законы Кеплера, все, что нам нужно, это два наблюдения положения планеты, и мы сможем предсказать ее орбиту.
Эти открытия вымостили дорогу Ньютону. Великим прозрением Ньютона было увидеть, что сила, которую Солнце оказывает на планеты, является той же самой, как и сила гравитации, которая удерживает нас на Земле, и потому объединить физику небес с физикой на Земле.
Конечно, идея силы, испускаемой от Солнца на планеты, была абсурдной для большинства ученых того времени. Они верили, что пространство пустое, там нет носителя, который мог бы переправлять такую силу. Более того, не было никаких видимых ее проявлений – никакой руки, протянувшейся от Солнца до каждой планеты, – а невидимое ничто не может быть реальным.
Все это хорошие уроки для будущих объединителей/унификаторов. Первый в том, что математическая красота может ввести в заблуждение. Простые наблюдения, сделанные на основании данных, часто более важны. Другой урок в том, что корректные унификации имеют следствия для явлений, о которых не подозревали в момент, когда унификация придумывалась, как в случае с применением законов Кеплера к лунам Юпитера. Правильные объединения также поднимают вопросы, которые могут показаться абсурдными в тот момент, но которые приводят к дальнейшим унификациям, как это было с постулатом Кеплера о силе, действующей от Солнца на планеты.
Самое важное, мы увидели, что реальная революция часто требует нескольких новых предложений по унификации, идущих вместе, чтобы поддерживать друг друга. В революции Ньютона было несколько предложенных унификаций, которые одновременно одержали триумф: объединение Земли с планетами, объединение Солнца со звездами, объединение покоя и равномерного движения и объединение гравитационной силы на Земле с силой, путем которой Солнце влияет на движение планет. Проще говоря, ни одна из этих идей не могла бы уцелеть, но вместе они побили своих противников. В результате получилась революция, которая трансформировала каждый аспект нашего понимания природы.